![]() を今までどおり実数体とする. 実数係数の文字
を今までどおり実数体とする. 実数係数の文字 ![]() の多項式の全体を
の多項式の全体を
明らかに![]() は体の定義のうち,「乗法の逆元の存在」以外のすべてを満たす.
は体の定義のうち,「乗法の逆元の存在」以外のすべてを満たす.
「乗法の逆元の存在」以外のすべてを満たすものを環という.
![]() を「実数体上の多項式環」という.
を「実数体上の多項式環」という.
そこで多項式 ![]() を多項式
を多項式 ![]() で割った余りを
で割った余りを ![]() と書くことにし,
集合
と書くことにし,
集合 ![]() を
を![]() で割った余りの集合
で割った余りの集合
史織
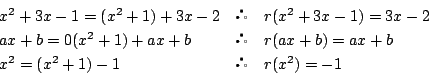
南海
割り算の余りなので
だから集合 ![]() の四則演算を,多項式の四則演算そのもので定めれば,
体の条件のうち除法の逆元の存在を除いてその他が成立することは
ほとんど自明である.
の四則演算を,多項式の四則演算そのもので定めれば,
体の条件のうち除法の逆元の存在を除いてその他が成立することは
ほとんど自明である.
そこで気になる人は実際に確かめてもらうことにして,逆元の存在証明に進もう.
史織
求める ![]() を
を![]() と置きます.まず
と置きます.まず![]() を求めます.
を求めます.
なんだかこれって,複素数の積
で,
これから ![]() と
と ![]() を
を ![]() と
と ![]() で表すと
で表すと
つまり
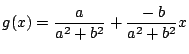
南海
かくして ![]() には乗法に関する逆元が存在した.
には乗法に関する逆元が存在した. ![]() も体である.
も体である.
実数 ![]() に対して
に対して
![]() である.だから
である.だから ![]() で割った余りとしての
で割った余りとしての ![]() や1を
や1を ![]() や
や ![]() と書くと
と書くと
史織
南海
さよう.正確にいうと,![]() から
から ![]() への写像
への写像
先に作った ![]() と今回の
と今回の ![]() ももちろん体として同型である.つまり
ももちろん体として同型である.つまり
![]() から
から ![]() への写像
への写像
結局教科書の複素数の定義と同型である2つのモデルが構成できたわけだ. このモデルは2つとも,確かに存在している.
複素数体 ![]() は,このようなモデルから平面の点であるとか多項式の余りであるとかの
他の要素を捨象し,体としての構造を抽出したものといえるのだ.
は,このようなモデルから平面の点であるとか多項式の余りであるとかの
他の要素を捨象し,体としての構造を抽出したものといえるのだ.
「みかん1個」と,「スプーン1本」などから数「1」が抽出されたように,
![]() は
は ![]() や
や ![]() から抽出されたものを表す記号である.
から抽出されたものを表す記号である.
それは勝手に作ったものではない.つまり![]() は
「平方すると
は
「平方すると ![]() になる新しい数を一つ考え」たのではなく,
抽出されたものとして確かに存在しているのだ.
になる新しい数を一つ考え」たのではなく,
抽出されたものとして確かに存在しているのだ.
史織
「みかん1個やスプーン1本の〈1個〉や〈1本〉は存在するが〈1〉は存在しない」などとは
思いません.確かに 1 はあるものとして計算しています.
それと同じように ![]() も存在するのですね.
も存在するのですね.
南海 その通りだ.
さてもう一つ行列を用いる構成方法がある.それは演習にする.
2次行列の部分集合 ![]() を次のように定める.
を次のように定める.
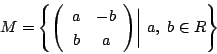
![]() において加法,乗法は2次行列の加法,乗法をそのまま用いるとする.
において加法,乗法は2次行列の加法,乗法をそのまま用いるとする.
このとき次の問に答えよ.
これに関係する入試問題を一つ .
行列
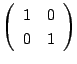 を
を ![]() で表し,行列
で表し,行列
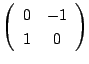 を
を ![]() で表す.
複素数
で表す.
複素数
![]() に行列
に行列 ![]() を対応させる.例えば,複素数
を対応させる.例えば,複素数 ![]() には行列
には行列
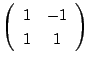 が対応する.
が対応する.
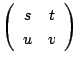 の形に表せ.
の形に表せ.
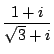 に対応する行列を
に対応する行列を