next up previous
次： 数列は関数だ 上： 関数 前： 合成関数，逆関数

対応

南海　 写像や関数の定義では「ある対応によって」とか「一つずつ対応している」など， 「対応」という言葉が使われている．「対応」とはどういうことか．

史織　 えっ，「対応」の定義ですか?

南海　 というより，「対応」とは結局どのようなものかということをここで考えようということなのだ． $y=f(x)=x^2$という関数で$x=2$と$y=4$は対応しているが$x=2$と$y=0$ は対応していない．

逆にいえば 集合${\mathsf A}$の任意の要素 $a$ と 集合${\mathsf B}$の任意の要素 $b$ が対応しているか 対応していないかを明確に決める条件が存在すれば，それによって 集合${\mathsf A}$と集合${\mathsf B}$の間の「対応」が定まる．

史織　 そうすると写像の定義の冒頭は次のようにならなければならない．

集合${\mathsf A}$の任意の要素 $a$ と 集合${\mathsf B}$の任意の要素 $b$ がある条件をみたすとき $a$ と $b$ は「対応している」という．

二つの集合 ${\mathsf A},\ {\mathsf B}$ において，

\begin{displaymath} {\mathsf A} のどの要素にも, {\mathsf B} の要素が\textbf{一つずつ}対応している \end{displaymath}

とき，この対応を${\mathsf A}$から${\mathsf B}$への写像という．

史織　 対応というのは大変広い意味がありそうですね．しかし高校数学ではあまり必要ないようです．

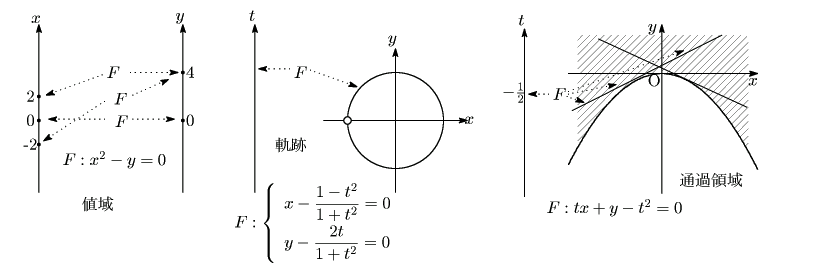
南海　 ところがそうではないのだ．話は逆で高校数学のもっとも基本的な内容が実は「対応」の 問題として統一的にとらえることができるのだ． 少しその話をしよう．値域，軌跡，通過領域に関することだ．

史織　 値域つまり関数のとる値の範囲，軌跡つまりある条件を満たす点の集合で曲線になるもの， 通過範囲つまりある条件を満たす点の集合で領域になるもの， などを求める問題はどれも同じ形をしていて解き方も基本は同じだということは知っています．

南海　 値域や軌跡，通過範囲が解き方が同じというだけではなく， 問題そのものが同じなのだということである． それを少し説明しよう．

${\mathsf A},\ {\mathsf B}$ を数直線や座標平面，またはその部分集合とする．

${\mathsf A}$ の要素を動く変数 $X$ と ${\mathsf B}$ の要素を動く変数 $Y$ の間に 関係式で対応が定まっているとする．この関係式を $F(X,\ Y)=0$ と象徴的に書こう． 象徴的というのは，式が一つとはかぎらないからである． また，$X$ や $Y$ と大文字を使ったのは，$X=(2,\ 3)$ のような平面の点のこともあるからだ． 1変数のときは小文字を使う．媒介変数には $T$ が用いられることも多い．

  1. ${\mathsf A},\ {\mathsf B}$ が実数で$f(x)=x^2$とし関数$y=f(x)$を考える． このとき対応を定める $F$ は $F(x,\ y)=-x^2+y$となる． $x=2$ と $y=4$ は対応しているが$x=3$ と $y=4$ は対応していない．

    $x$ が実数を動くとき$F(x,\ y)=0$ によって各 $x$ と対応するような $y$ の集合 $V=\{\ y\ \vert\ y \ge 0\}$ が値域である．

  2. ${\mathsf A}$ が実数で ${\mathsf B}$ が $xy$ 平面．

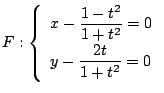    二つの式 $F:\left\{\begin{array}{l}x-\dfrac{1-t^2}{1+t^2}=0\\ y-\dfrac{2t}{1+t^2}=0 \end{array}\right.$ で実数 $t$ と対応するような $xy$ 平面の部分集合が軌跡そのもの．

  3. ${\mathsf A}$ が実数で ${\mathsf B}$ が $xy$ 平面．

    一つの式$F:tx+y-t^2=0$ で対応を定める． $t=1$ と $(2,\ -1)$ は対応している． $t=1$には$x+y-1=0$ で定まる $xy$ 平面の直線上の各点が対応する．

    実数$t$ が実数を動くとき, 対応する点よりなる$xy$ 平面の部分集合が通過領域．

史織　 そうか．確かに高校数学の対象のほとんどは「対応」だ．

南海　 値域，軌跡，通過領域はどれも，集合${\mathsf A}$ に対して

\begin{displaymath} {\mathsf A}の要素と対応する{\mathsf B}の要素全体 \end{displaymath}

という形をしている．対応の条件を$F(T,\ X)=0$とし，これを集合で書けば

\begin{displaymath} {\mathsf V}=\{X\vert X \in {\mathsf B},\ F(T,\ X)=0となるT \in {\mathsf A} が存在する\} \end{displaymath}

となる．この $V$ があるときは値域であり，軌跡であり，通過領域と言われる，ということだ．

史織　 「値域」，「軌跡」とか「通過領域」とかいっても要するに「一定の条件を満たす点の集合」 のことなのですね． だから， $T$ が${\mathsf A}$に存在する条件として ${\mathsf V}$ が求まるのです．

これが ${\mathsf V}$ を定めるいちばん論理的な方法です．

南海　 もちろん論理的にこうだからと言って，いつも求まるともかぎらないのだが，この論理的な考え方が高校生には 大切だ．


Aozora Gakuen