次： 座標の方法 上： 関数 前： 対応

数列は関数だ

南海　 数列は関数だ．

史織　 定義域が自然数の関数が数列でした．数列 $\{a_n\}$ に対して $f(n)=a_n$ と定めると 自然数に対して定義された関数 $f(n)$ が得られます．

南海　 そうなのだ．数列を関数の立場から考えることが大切だ．

自然数に対して定義された関数 $f(n)$ を解析する基本は

$$\Delta f(n)=f(n+1)-f(n)$$

を解析することである．これはつまり階差数列である．

階差を取る作用は 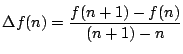$\Delta f(n)=\dfrac{f(n+1)-f(n)}{(n+1)-n}$ としてみればわかるように， $n$ の増分1に対する平均変化率だ． 実は「階差をとる」ことを「差分する」ともいうのだが， これは言うまでもなく「微分する」と対応する言葉の使い方だ．

ついでながら階差数列からもとの数列を見出す

$$f(n)=f(1)+\displaystyle \sum_{k=1}^{n-1}\Delta f(k)$$

という操作は，関数 $f(x)$ では，原始関数を求める積分そのものだ． ついでに言えばこの操作を「和分する」という．「積分する」に対応する言葉だ．

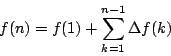
このような観点から，いくつかの問題を紹介しよう．いずれも高校数学としては難問である．

演習 13       解答13

$f(x)$ を実数係数の $k$ 次の整式とする. 任意の整数 $n$ に対して $f(n)$ が整数値をとるための条件を次の方法で考えよ.

1. 『任意の整数 $n$ に対して, $f(n)$ が整数となるための必要十分条件は
   $f(x)$ の $k+1$ 個の連続する整数 $m,\ m+1,\ \cdots,\ m+k$ に対する値
   
   $$f(m),\ f(m+1),\ \cdots,\ f(m+k)$$
   
   
   がすべて整数値である』ことを示そう.
   1. $n$ 次の整式 $f(x)$ に対して
      
      $$f(x+1)-f(x)$$
      
      
      は $n-1$ 次以下であることを示せ.
   2. 冒頭の命題を数学的帰納法で示せ.
2. 0以上の整数 $l$ に対し
   
   $$u_l(x)=\dfrac{x(x-1)\cdots(x-l+1)}{l!}\ (l\ge1のとき),\quad l_0(x)=1$$
   
   
   とおく.
   1. $k$ 次多項式 $f(x)$ は実数 $c_0,\ c_1,\ \cdots,\ c_k$ を用いて次のように表されることを示せ.
      
      $$f(x)=\sum_{l=0}^k c_l\cdot u_l(x)$$
      
      

   2. 任意の整数 $n$ に対して $f(n)$ が整数となるための必要十分条件は, $f(x)$ を上のように表したとき, $c_0,\ c_1,\ \cdots,\ c_k$ がすべて整数となることであることを示せ.

演習 14       解答14

実数係数の$k$ 次多項式 $f(x)$ が

$$f(0)=1,\ f(1)=2,\ f(2)=4,\ \cdots,\ f(k)=2^k$$

をみたしている．このとき，$f(k+1)$ の値を求めよ.

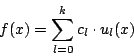
史織　 ありがとうございました．