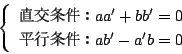さて第二の直線の作り方はベクトルの直交条件を使う.
![]() でない二つのベクトル
でない二つのベクトル
![]() と
と
![]() が直交している条件は,二つのベクトルのなす角が
が直交している条件は,二つのベクトルのなす角が
![]() ,
つまり内積が0ということなので,
,
つまり内積が0ということなので,
そこで,定点
![]() をとおり,ベクトル
をとおり,ベクトル
![]() に直交する直線
に直交する直線 ![]() の方程式を求めよ.
の方程式を求めよ.
史織
これは教科書にも載っています.直線上の任意の点
![]() をとる.
をとる.
二つのベクトル
![]() と
と
![]() が直交するので内積が0.
が直交するので内積が0.
![]() なので
なので
このベクトル
![]() のことを
直線
のことを
直線 ![]() の法線ベクトルという.
の法線ベクトルという.
南海
その通り.直線 ![]() とベクトル
とベクトル ![]() は平面上でたがいに直交している.
は平面上でたがいに直交している.
二つの直線
![]() に対して二つの法線ベクトル
に対して二つの法線ベクトル
![]() ができるが,もとの二直線が直交または平行であるのに応じて,それぞれの法線ベクトルも
直交または平行であるから,上の二直線の
ができるが,もとの二直線が直交または平行であるのに応じて,それぞれの法線ベクトルも
直交または平行であるから,上の二直線の