このアルキメデスの数学に関する仕事のなかで最も有名なのは,いろんなものの面積や体積を求め
たことだ.球の表面積 ![]() を求めたのもアルキメデスである.その方法は,面積を小さ
な部分に分け加える,という区分求積法であった.
を求めたのもアルキメデスである.その方法は,面積を小さ
な部分に分け加える,という区分求積法であった.
この時代は,もちろん座標の方法もないし,関数を式に表すことも知られていない.彼は放物線で 囲まれた図形の面積を次のように求めた.一応座標に入れて説明する.アルキメデスはもっと図形 的にやったのである.
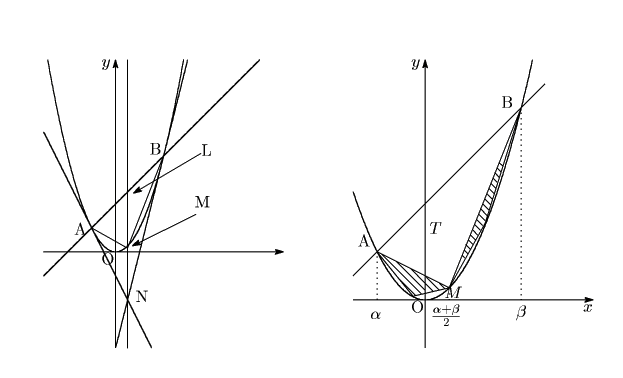
![]() 座標が
座標が ![]() と
と ![]() の
の ![]() 座標の中点と一致する点を
座標の中点と一致する点を
![]() ,
, ![]() と
と ![]() での接線の交点を
での接線の交点を ![]() とする.このとき一般に
とする.このとき一般に
そこで
![]() ,
,
![]() ,求める面積を
,求める面積を ![]() とし,
とし,
![]() の面積を
の面積を ![]() とすると,
とすると,
彼は次のように示した.右側の図の斜線部分の面積はちょうど ![]() である(なぜか?).
ここで斜線部分に対して同じ操作を行うとさらに
である(なぜか?).
ここで斜線部分に対して同じ操作を行うとさらに
![]() 面積が増える.このようにして
次々に加えていくとこの面積の和は
面積が増える.このようにして
次々に加えていくとこの面積の和は ![]() に近づく.つまり
に近づく.つまり
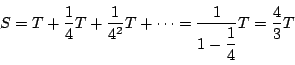
![]() はいくらになるか
はいくらになるか
史織
![]() の座標は
の座標は
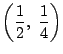 なので
なので
南海 だから
昔の人はいろんな面積をこのような区分求積法で求めた.日本の和算家も求めている.
史織 わー,たいへんですね.
南海 そこで「微積分の基本定理」なのだ.