同じく『問題新集 微分・積分基本500選』(科学新興社)のまとめに次のように書かれている.
微積分の基本定理
関数が区間
で連続ならば,
の点
に関して,
の関数
したがって,その結果として
関数が区間
で連続で,
が
の原始関数ならば,
が成り立つ.
史織 ③の極限が ![]() が連続なら存在するのですか.
が連続なら存在するのですか.
南海 そうだ.理論的にはそこが肝心なところなのだ. その証明自体は高校範囲を超える.
大切なことは,積分は ③の和の極限として定まり,
その意味は ![]() と
と ![]() 軸で囲まれた図形の符号つき面積だ,ということだ.
軸で囲まれた図形の符号つき面積だ,ということだ.
③が存在しているとき, その和の極限である「符号付き面積」が実は原始関数から求まる, というのが「微積分の基本定理」なのだ.それを示そう.
関数 ![]() が区間
が区間 ![]() で連続で
で連続で ![]() とする.
とする.![]() の点
の点 ![]() に関して,
に関して, ![]() の関数
の関数
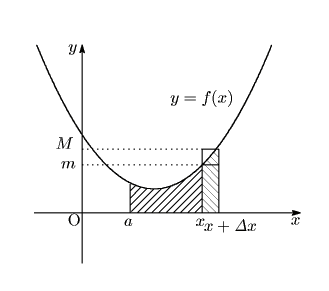
![]() に対して増分
に対して増分 ![]() をとり小区間
をとり小区間
![]() での最小値を
での最小値を
![]() ,最大値を
,最大値を ![]() とする.
とする.
したがって
![]() の原始関数を
の原始関数を ![]() とする.
とする.
史織 すると「 ![]() と
と ![]() 軸に囲まれた図形の面積は,
軸に囲まれた図形の面積は, ![]() の
原始関数でも求めることができる」ということが,「微積分の基本定理」なのですね.
の
原始関数でも求めることができる」ということが,「微積分の基本定理」なのですね.
南海 そうだ.
放物線 ![]() と 放物線上の2点
と 放物線上の2点
![]() を結ぶ直線で囲まれた図形の面積は,
アルキメデスのように区分求積をしなくても, 2点を結ぶ直線の式
を結ぶ直線で囲まれた図形の面積は,
アルキメデスのように区分求積をしなくても, 2点を結ぶ直線の式 ![]() を出して
を出して
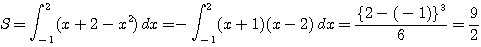
リーマン和に関する入試問題を紹介しておこう.