はじめに紹介したパスカルとフェルマの往復書簡中で議論されている問題を考えよう. 2人は,ド・メレという人から出された「分配問題」を議論し,いろんな方法で考えている. 一般的な解法はパスカルが出している.
問題を一般化しよう.
今,A と B が互いに円ずつ出して勝負している.Aが勝つ確率は
で Bが勝つ確率は
であるとする.
である. 1回勝つと1点もらえて,先に
点獲得した方が優勝し賭金
円をもらう. A が
点獲得しBが
点獲得しているときに,やむを得ない事情で勝負を中止しなければならなくなった.
円をどのように分配すべきか.
史織
Aが勝つためにはあと![]() 点,Bが勝つためにはあと
点,Bが勝つためにはあと![]() 点必要です.これをもとに,この後引き続いて
勝負をしたとして,Aの勝つ確率,
点必要です.これをもとに,この後引き続いて
勝負をしたとして,Aの勝つ確率,![]() の勝つ確率を計算し,その比に応じて分配するしかないと思います.
の勝つ確率を計算し,その比に応じて分配するしかないと思います.
南海
そうだ.
つまり,この時点でAのもらえる期待値,Bのもらえる期待値を計算すると言うことだ.
![]() とおいて計算式を作ってほしい.
とおいて計算式を作ってほしい.
史織
最大![]() 回勝負すればいずれかの勝ちが決まります.そこで
回勝負すればいずれかの勝ちが決まります.そこで![]() とします.
Aが
とします.
Aが![]() 回勝つまでにBが
回勝つまでにBが![]() 回勝つとすると,
その事象は,
回勝つとすると,
その事象は,![]() 回中
回中![]() 回Bが勝ち,
回Bが勝ち,![]() 回目にAが勝つ事象なので,
その確率は
回目にAが勝つ事象なので,
その確率は
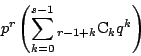
最初の問題では
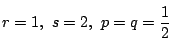 なので,Aが勝つ確率は
なので,Aが勝つ確率は
南海 パスカルはこの計算をするのにいわゆる「パスカルの三角形」を使っている.
史織 パスカルの三角形は確率の計算で使われたのですか.
南海 パスカルはこれらの研究を完全な論文にまとめようとする意図をもっていたらしい. 後にパリ科学アカデミーとなる機関にあてた1654年の書簡の中で,パスカルはつぎのように述べている.
正当に競い合っている演技者双方に,不確定な未来がつねに正確に配当されるようにするための, 理にかなった計算は,うまくできませんでした. 確かに,偶然の推理を探究すればするほど,調べてわかることはほんのちょっぴりしかありません. あいまいさ,例えばくじ引きという事象は,必然性よりむしろ全く偶然性に左右されることが自然なのでして, それによって報酬が分配されるのであります. それゆえ,いままではそのような事柄は不確かなものだとしてきました. しかし,いま経験にさからってまでも偶然を支配している論拠をはっきりとさせたいと存じます. もち論,そのようなことを幾何学的方法によって学問的な保証をとりつけ, 確実性がこの種の偶然性にも関係している事実を大胆に打ち出そうと思っています. そして,数学が不確実な事象をひき起こすサイコロと結びついていることを示し, 加えて偶然と確実の相矛盾したものを統一的にとらえ, 統一されたものは偶然とも確実とも指名できないものでありますから, “サイコロの幾何学"という表題の本を手にとった人はきっとびっくりするに違いないと思います.
この計画は実現せず,パスカルは1662年に39歳の若さで亡くなる. だが,この確信に満ちた文章は確率論の宣言といってよいほどのものである. ここに確率論は誕生した.