確率変数![]() は
は
![]() の値を取り,
その確率が
の値を取り,
その確率が
![]() であるとする.
つまり
であるとする.
つまり
![]() であるとする.
であるとする.
確率変数![]() は
は
![]() の値を取り,
その確率が
の値を取り,
その確率が
![]() であるとする.
つまり
であるとする.
つまり
![]() であるとする.
であるとする.
値![]() を確率
を確率
![]() でとる確率変数を,確率変数
でとる確率変数を,確率変数![]() と
と![]() の和といい,
の和といい,![]() と書く.
と書く.
値![]() を確率
を確率
![]() でとる確率変数を,確率変数
でとる確率変数を,確率変数![]() と
と![]() の積といい,
の積といい,![]() と書く.
と書く.
確率変数![]() の期待値
の期待値 ![]() は
は ![]() と一致する.
と一致する.
史織
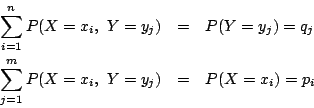
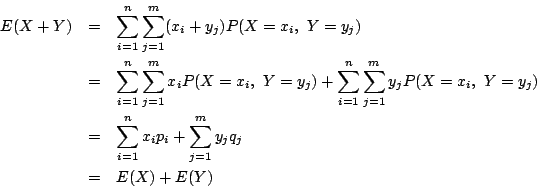
南海
これは要するに,英語と数学の合計の平均を求めるのに,先にそれぞれの合計を出しその平均をとろうと,各教科の平均を出してから加えようと,同じ結果になるということである.
![]() は何かと便利な公式であるので,使ってみよう.
は何かと便利な公式であるので,使ってみよう.
3個の変量![]() のときも
のときも
史織
期待値は結局根元事象の全体にわたる和であるという観点から
![]() を示せませんか.
を示せませんか.
南海 できる.やってみてほしい.
史織
![]() の値が
の値が![]() であり,
であり,![]() の値が
の値が![]() であるような事象を
であるような事象を![]() とおく.すると標本空間
とおく.すると標本空間![]() は
互いに排反な事象
は
互いに排反な事象![]() の和になる.そして
の和になる.そして
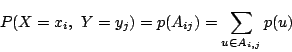
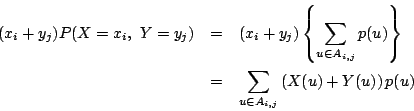
したがって
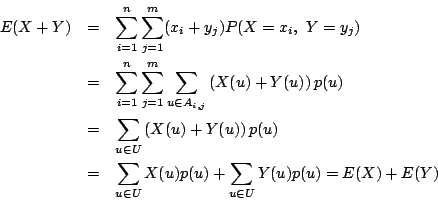
ここで期待値の和を問う過去問題を紹介しよう.
ある人がサイコロを振る試行によって,部屋A,Bを移動する.
サイコロの目の数が1,3のときに限り部屋を移る.
また各試行の結果,部屋Aに居る場合はその人の持ち点に1点を加え,部屋Bに居る場合は1点を減らす.
持ち点は負になることもあるとする.
第![]() 試行の結果,部屋A,Bに居る確率をそれぞれ
試行の結果,部屋A,Bに居る確率をそれぞれ
![]() と表す.
最初にその人は部屋Aに居るものとし(つまり,
と表す.
最初にその人は部屋Aに居るものとし(つまり,
![]() とする),持ち点は1とする.
とする),持ち点は1とする.