まず上のように1あたり量を導入し,乗法との関係を明らかにする.
分数の積の授業が目的であったので,量の導入も最初からではなかった.しかし,それでも高校生にとって1あたり量を理解することは困難ではなかった.(何々)が(いくつ)というのは,分数「2/5」を「5分の2」と読む日本語に助けられている.この分数の理解は(5分の1)が(2つ)と読んでいるのであるから,1あたり量もこの分数の読解から自然に導かれる.
太郎
2%の濃度の食塩水が400gあるとき,その中に含まれている塩の量は
南海
さまざまの量があるが,1あたり量と全体量は次のような図式になる.
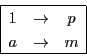
太郎
この1や![]() などは数ですか.それとも量ですか.
などは数ですか.それとも量ですか.
南海 教えているときは量だ.単位をつけることが多い.しかし高校生に教えるときは明確にはいわなかったように思う.高校生には数と量の境界を明確にはしないままであったと思う.
さてこのとき,![]() を
を![]() と
と![]() の積という.つまり乗法とは
の積という.つまり乗法とは
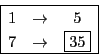
密度がということになる.のものが体積
あるとき,重さは
ある,
このようにして積を考えたのだ.しかしいま考えれば,これは積の定義とは言えない.数の積は量においてはこのように(1あたり量)と(いくら量)から(全体量)を求まる「計算」として解釈できるが,なぜそこに35が来るのかの内在的な意味づけは出来ない.
2012〜2013年に,積の順序という問題が新聞紙上などでふたたび取りあげられた.学校では(1あたり量)×(いくら量)=(全体量)の順に書くことを教え,逆に書くと間違いとされる,という問題だ.これに対して「こだわるとかえって混乱を来す」や順にこだわるのは「ナンセンスだ」と言う意見が紹介されている.
これらの報道を読み,またウエブ上に現れた意見などを見ると,(1あたり量)×(いくら量)という考え方との関連で,ここにはいくつもの考えるべき問題がある.
このあたりにいろいろ考えるべきことがあり,しかもそれが追究されないままに,長い長い時間が経過した.
太郎 負の量を考えるのですか.
南海
面積なんかでも負の面積もある.
![]() で3点
で3点
![]() が反時計回りにまわっているとき面積を正,反時計回りにまわっているとき面積を負とする,と決めればよい.原点と2点
が反時計回りにまわっているとき面積を正,反時計回りにまわっているとき面積を負とする,と決めればよい.原点と2点
![]() で
で
![]() の面積
の面積![]() を正負のある量としてこの意味で定義すると
を正負のある量としてこの意味で定義すると
移動量もまた東方向への移動を正,西方向への移動を負とする.
太郎
わかってきました.
![]() は
は
東方向へ秒速を意味します.これはで歩いている人が,
秒間後にはどこにいるか.
西方向へ秒速と同じことなので,今いるところから東へで歩いている人が,
秒間前はどこにいるか.
南海 今回,足立恒雄先生の『数とは何か そしてまた何であったか』(2011年,共立出版)第1章の3節,「負数」に教えられたのであるが,自然数をものの個数として正の数でとらえ,正の数から考えはじめるのは,西洋固有の伝統であって,東洋においては,数でとらえるものは,ものの個数ばかりでなく,場所,位置,事物(財産と負債のような)などがあり,正の数と負の数ははじめから考えられていた.16世紀のインドの数学の本の中に「負数と負数をかけ合わせると正数を得ることは羊飼いや牛飼いでも知っている」とあるそうだ.
太郎 そうか.私たちは学校教育で正数を基本とする授業を受けてくるから,負数と負数の積が難しいように考えるが,量をはじめから負も含めて考えれば,これは難しいことではないのか.
南海 これからこのような問題も見直されてゆかねばならない.
水道方式では,さまざまの量とその数化の間に中間的な抽象物として,タイルを用いる.これは優れた方法だった.量はそれぞれ具体的な量である.しかしそこに量としての共通性がある.この量としての共通性を目に見える形にしたのがタイルだ.私もかつてこの方法を学び授業で使った.
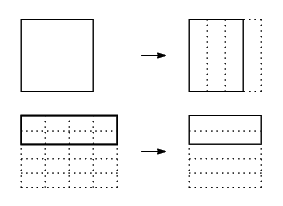
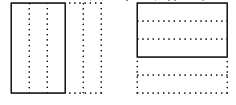 タイル法はとくに分数に数化される量を一般的に表すのに優れていた.正方形の1つのタイルが1を表すとき,分数
タイル法はとくに分数に数化される量を一般的に表すのに優れていた.正方形の1つのタイルが1を表すとき,分数![]() に対応する量を表すタイルは
右のようになる.
に対応する量を表すタイルは
右のようになる.
太郎 縦に分けても横に分けてもかまわないのですね.
分数の積ですが,例えば
![]() なら1あたり
なら1あたり![]() であるとき,
であるとき,![]() にはいくらの量が対応するかなので,
にはいくらの量が対応するかなので,
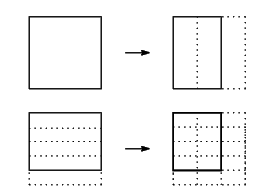
のように,1つのタイルを![]() に分けたうちの
に分けたうちの![]() が対応することがわかります.
が対応することがわかります.
南海 私も若いときそのような授業をした.確かにこのモデルにおいて,分数の積の計算方法は説明できる.当時は授業を成り立たせることで精一杯で,それ以上には考えられなかった.

太郎
積の場合と同様に考えます.例えば
![]() を第1の方で考えると全体から
を第1の方で考えると全体から![]() だけとったなら
だけとったなら![]() になるような元のタイルなので,
になるような元のタイルなので,
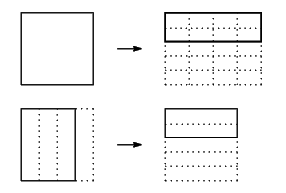
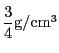 のものが
のものが
南海 もちろん実際の授業ではもっとていねいにした.割り算もまず個数の場合で割り算になることを理解してから,そのうえで分数の乗除に入った.
こうして分数計算の根拠についての授業を終え,そこからクラスとして考えてゆくということができた.もちろん,実際はそんなに簡単ではなかった.
その後,関数のところでも水道方式の世話になった.関数の概念は,今も高校生が理解しづらいものだが,ブラックボックスの図を作り「働き」としての関数を教えていった.教えることについて実に多くのことが学べた.
2005年になって,その頃の教え子に再会した.卒業以来28年ぶりだった.すぐ昔の話になり「高校でもう一度分数を習うとは思っていなかった」,「ブラックボックスの話はおもしろかった」などよく昔のことを覚えていてくれた.印象に残るものであったことはまちがいない.
私は教師になったばかりの頃にこのような授業をした.私の働いた高校では,地元のいわゆる障害生学級卒業の子も受け入れていた.私自身が,教員になってその問題に取り組んだ.そして授業そのものは,取り出しでやっていた.そこでの授業でも,量から入ることではじめて計算方法も定着するという経験もした.
その後私は高校教員を辞め,他の仕事につき,それからまた高校生に教える仕事に戻ってきた.このときにやった授業をもういちど振り返りたいと思いながら,なかなかできなかった.
水道方式はこのように確かに有効な教育方法であったが,数学としてこれを見直すことが私自身の宿題で,青空学園でいろいろ作ってきたのも,その宿題に答えようとすることという意味もあった.ようやく2008年にはじめて書いてみることが出来たが,量の捉え方は昔の水道方式のままであった.