次: 参考書 上: 不完全性定理 前: 形式化された数学

ゲーデルの対角線論法

不完全性定理

南海　 先にあげた不完全性定理を，再掲しよう．

定理 6 (第一不完全性定理)   自然数論を含む帰納的に記述できる体系が，無矛盾であればその体系は完全ではない．つまり，真ではあるが，証明も反証もできない命題が存在する．

定理 7 (第二不完全性定理)   算術を含む形式化された体系が無矛盾であれば， 体系内部で体系の無矛盾性を証明することはできない．

その証明の実行はここではできないが，その骨子を話してゆきたい．

さて，ゲーデルの著『「プリンキピア・マティマティカ」やその関連体系での形式的に決定不可能な命題について』は次のようにはじまる．

序論

よく知られているように，数学はいっそうの厳密化をめざして進み，広い範囲の数学を形式化している．その結果，証明はいくつかの機械的な規則の運用によって遂行できるようになった． これまでのところもっとも包括的な体系は，「プリンキマテマティカ，Principia Mathematica (PM)」の体系と，ツェルメロ−フランケル(Zermelo-Frankel)による集合論の公理体系(近年ノイマンによって拡張された)である．

これら二つの体系は，大変包括的なもので，今日数学で用いられる証明の方法のすべてがそのなかで定式化されている．つまり，いくつかの公理と推論の規則に還元されている．したがって，これらの公理と推論規則は，関連した体系のなかでとにかく何らかの方法で形式的に表現されたすべての数学の問題の真偽を決定するのに十分であろうと考えられる．

以下に示すように，これは真実ではない．いずれの体系においても，比較的単純な自然数の問題で，それらの公理からは決定することができないものが存在する．このことは，構成された体系のいくつかの個別の性質によるものではなく，非常に一般的な形式体系において成り立つ．特に，先の体系に有限個の公理をつけ加えることで構成されるすべての体系でも，それによって偽な命題が証明されることにならないかぎり，成り立つ．(以下略)

拓生　 完全ではない，ということは，体系が矛盾ないものであれば，そこには，真ではあるが証明できない命題が存在する，ということですね．

いったいどのようにしてそんなことを示すのですか．

南海　 それが本質的に対角線論法なのだ．

ただそこに至るまでには，いくつかの準備が必要なのだ．それはいろんな書物に書かれている． ここでは，参考書『ゲーデルは何を証明したか』によって，ゲーデルの原論文をより簡明化した，ロッサーによる展開の骨子だけを話そう．

ゲーデル数

南海　 まず，自然数を含むある数学の体系を形式化(記号化)する．

そこで，次のように体系の対象式または関係式である記号の列$A$と整数の部分集合$G$に対して，整数$g(A)$を一対一に対応させる．整数$g(A)$を$A$のゲーデル数という．

つぎのように構成する．まず論理記号に次の数を対応させる．

$$\begin{array}{\vert c\vert c\vert c\vert} \hline 論?... ...&右かっこ\\ ，&10&コンマ\\ \hline \end{array}$$

さらに変数として，数値的な変数 $x,\ y,\ \cdots$には10より大きい素数を，文書をまとめる文書的な変数 $p,\ q,\ \cdots$には10より大きい素数の平方を，述語的な変数 $P,\ Q,\ \cdots$には10より大きい素数の立方を，ゲーデル数の値とする．

これだけで，命題も論証も書くことができる．

これに対して，体系でのあらゆる論証について，それを記号列で表したうえで，構成要素に対応するゲーデル数をまずとり，その個数だけの素数を小さい方から順に並べ，構成要素のゲーデル数を，素数のべきにつけてすべてかけあわせるのだ．

この方法で，体系での命題 $(\exists x)(x=\mathrm{s}y)$は何が対応するか．

拓生　 意味は，「$y$の次の数$x$が存在する」ですね．

南海　 これを記号で表すと

$$(\exists x)(x = \mathrm{s} y)$$

となる．

拓生　 それぞれのゲーデル数は

$$8,\ 4,\ 11,\ 9,\ 8,\ 11,\ 5,\ 7,\ 13,\ 9$$

ですから

$$g((\exists x)(x=\mathrm{s}y)) =2^83^45^{11}7^911^813^{11}17^519^723^{13}29^9$$

ですか．

南海　 ある自然数$n$がゲーデル数であるかどうかは，その数を因数分解したときに，まず素数が順にすべて入っていることが必要で，それが満たされれば，指数が再びゲーデル数であるかを見ていけば，有限回の操作で，判断できる．

拓生　 実際は大変です．数3のゲーデル数$g(3)$は，…．
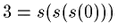$3=g(g(g(0)))$ですから構成要素のゲーデル数は $7,\ 8,\ 7,\ 8,\ 7,\ 8,\ 6,\ 9,\ 9,\ 9$なので，これから作ればいいのか．

証明不能命題

南海　 そうだ．重要なことは，次のことが成り立つということだ．

$x=g(A)$と$y=g(B)$に対して，

$$AはBの証明である$$

が成立するとき，そしてそのときにかぎって成立するような， 2つの整数$x$と$y$に関する算術的関係式が存在する．

これをゲーデルは，40以上の関係式を定義しながら，その上に構成できることを示した．それ自身が数学の作業であるが，その内容をここで展開することはできない．

いずれにせよ「$A$は$B$の証明である」のような言明を超数学的言明といおう， また「証明である」ということは，はじめの公理から結論にいたる論証の列が存在することだ．

拓生　 記号列$A$の末尾に$B$があるということですか．でも，どんな問題も証明できるけれども実際に解けるとはかぎらない．

南海　 ここでいったのは，証明の可能性であって，その論証過程を実際に見いだすことではない．5次方程式に根はつねに存在するが，解けるとはかぎらない．今，問題にしているのは，証明の可能性であって，証明が見いだせるかどうかではない．

拓生　 論証過程$A$もゲーデル数が対応するのですね．

南海　 実際の論証ははるかに複雑であるから，割れる割れないのような単純な算術関係ではない．ゲーデルは，先のような算術的関係式を構成する方法があり，それを実行することでえられることを示したのだ．それを $\mathrm{Dem}(x,\ y)$とする．

$$\begin{array}{ccc} &g&\\ 記号列&\to&ゲーデル?... ... 「AはBの証明」&\to&\mathrm{Dem}(x,\ y) \end{array}$$

次に道具として，記号 $\mathrm{sub}(m,\ p,\ a)$を導入する．

$m$を変数とし，数$m$が表す体系の記号列$M$，つまり$m=g(M)$をゲーデル数にもつ記号列$M$に対し,$M$の中の記号$p$が表す数変数に$a$を代入して得られる新しい記号列を$N$とする．

この記号列$N$のゲーデル数$g(N)$を $\mathrm{sub}(m,\ p,\ a)$と書き表す．用いるのは $\mathrm{sub}(y,\ 13,\ y)$だ．

拓生　 $13=g(y)$なので，ゲーデル数が$y$であるような記号列のなかの文字$y$に，値$y$を代入して得られる記号列のゲーデル数．

南海　 そう．$y$は変数で，この$y$は次に用いるように$x$の次の変数として用いている

そこで，新しい言明

$$(x)〜\mathrm{Dem}(x,\ z)$$

を考える．これ自身は，体系内の算術的な関係 $\mathrm{Dem}(x,\ z)$が，すべての数$x$で成立しないということを言明している．

もとの体系内の超数学的言明の方でいえば

$$すべての数 xについて，x=g(A)である各Aは，y=g(B)であるBの証明でない．$$

を意味する．

それに対応する自然数体系内の命題である．

以上の準備の後，

$$(x)〜\mathrm{Dem}(x,\ \mathrm{sub}(y,\ 13,\ y))$$

という言明を考える．

そこでこの言明のゲーデル数を$n$として，命題

$$(x)〜\mathrm{Dem}(x,\ \mathrm{sub}(n,\ 13,\ n))$$

を$G$とする．

拓生　 ここが対角線論法なのですね．

南海　 そうだ．このとき

$$g(G)=\mathrm{sub}(n,\ 13,\ n)$$

である．

なぜなら$n$と対応する命題は

$$(x)〜\mathrm{Dem}(x,\ \mathrm{sub}(y,\ 13,\ y))$$

であり，この式の$13$に対応する文字$y$に$n$が表す関係詞を代入したものが

$$(x)〜\mathrm{Dem}(x,\ \mathrm{sub}(n,\ 13,\ n))$$

で，この関係式と対応するゲーデル数が $\mathrm{sub}(n,\ 13,\ n)$に他ならないからである．

一方，式$G$は，ゲーデル数 $\mathrm{sub}(n,\ 13,\ n)$をもつ式は証明不能であるという超数学的言明を，体系内の算術的な命題で表したものである．実際，算術関係式$G$が証明可能であるとする．するとそれは，ゲーデル数 $\mathrm{sub}(n,\ 13,\ n)$をもつ式は証明不能である，つまり$G$が証明不可能であることを意味する．

逆に，$G$の否定が証明可能なら，ゲーデル数 $\mathrm{sub}(n,\ 13,\ n)$をもつ式は証明不能ではない，つまり$G$は証明可能になる．

$G$はその否定が証明可能なとき，そしてそのときにかぎり証明可能である．体系が無矛盾であるなら，これはあり得ない．つまり$G$もその否定も，証明可能ではない．

つまり

命題 1   算術が無矛盾なら， 式

$$G:(x)〜Dem(x,\ \mathrm{sub}(n,\ 13,\ n))$$

は証明可能でない．

が証明された．つまりこの命題は真である．

ところがこの命題自身を，算術の式に写像した式が$G$そのものであるから，$G$自身が真な式である．つまり，真ではあるが，証明も反証もできない命題の存在が示された．

これが第一不完全性定理6の証明の骨子である．

無矛盾性

南海　 体系が無矛盾ではない，ということは$S$もその否定$〜S$も共に証明されるような命題$S$が存在するということである．

一方，命題$S$が真であるとき，$〜S$は偽であり，その結果任意の命題$T$に対して

$$〜SならばTである．$$

は真な命題となる． したがってもし体系が無矛盾でなければ，任意の命題$T$が証明可能となる．よって，公理から導けない命題が一つでも存在すれば，その体系は無矛盾である．

逆に，体系が無矛盾であるとする．このとき，命題

$$二つの命題AとBに対して，A\vee Bは真である．$$

は明らかに証明可能ではない．

以上から，体系が無矛盾であることと，証明できない命題が存在することは同値である．

「証明できない命題が存在する」は，ゲーデル数とその間の関係式としては

$$(\exists y)(x)〜Dem(x,\ y)$$

と表される．この関係式を$A$としよう．

定理6によって，

$$AならばGである．$$

が成り立つ．ところがGは証明も反証もできない．したがって$A$もまた証明も反証もできない． つまり，第二不完全性定理7が証明された．

Bourbaki 『数学史』から

南海　 以上が，ゲーデルの論文のごく骨子である． もとより数学としては，自然数の体系の中で超数学的命題を表すために， 形式化された体系から自然数の体系への写像が存在し， さらに超数学的命題が自然数の中での命題に変換される， そのことを保障するために多くの関数を定義してゆかねばならない．

この問題を，ブルバキの『数学史』では，次のように定式化している．

体系の対象式または関係式である記号の列$A$に対して整数$g(A)$を一対一に対応させる． 体系の各証明$D$もまた記号列であるからこれに整数$h(D)$を対応させる．

体系内のある算術関係式$P(x,\ y,\ z)$で次の性質を持つものを構成する．$x,\ y,\ z$は整数である．かつ

1. $D$が$A(\lambda)$の証明ならば， $P(\lambda,\ g(A),\ h(D))$は体系で証明される． ただし，$A(x)$は体系の任意の関係式であり， $\lambda$は任意の具体的な整数である．
2. 整数$\mu$が$h(D)$という形でないか， または$\mu=h(D)$かつ$D$は$A(\lambda)$の証明でないときは， $〜P(\lambda,\ g(A),\ h(D))$が体系で証明される．

この構成が，超数学の算術化と対角線論法でおこなわれる．

$S(x)$を $〜(\exists z)P(x,\ x,\ z)$で定め， $\gamma=g(S(x))$とする． 体系が無矛盾なら$S(x)$もその否定$〜S(x)$も証明されない．

…

もちろんこの関係はそうなるように都合よく組み立てられたもので， どんな数学の問題とも自然に関連をもつようなものではない．

これと比べたらさらに一段と興味深いのは，連続体仮説もその否定もともに証明不可能という事実である．

ここにも書かれているように，その後ゲーデルや多くの人の努力によって，連続体仮説もその否定もともに証明不可能という事実もまた証明される．

拓生　 幾何の公理で平行線の公理が，他の四つの公理からは証明も否定の証明もされないというのと似ています．

南海　 そうだ．しかし，連続体仮説を公理として組み入れても，あるいはそれとは両立しない仮説を公理として組み入れても，これまでの所，新しい数学が出てきたわけではない．しかしそれはまだこれからの課題なのかも知れない．

また，ゲーデルの理論はその後，計算理論にも発展した．そのことはここでは展開できないが，指摘しておきたい．

いずれにせよ，数学的体系というのは絶対のものではなく，数学的現象，数学的真理を記述する方法なのであり，数学そのものはそれより広く，その体系内で完結することは出来ない． したがって，また体系は絶対のものではなく，数学の発展とともに変化し発展するものではないか．

ゲーデルの定理以降に数学の新たな枠組みを作ったフランスを中心とする数学者集団ブルバキは，このことを端的に次のように述べる．

もし，未来にそれ(現在の数学の枠組みとなっている公理的集合論)が破綻しても数学は必ずや新しい基礎を見つけるだろう

集合論の背理の発見から，ヒルベルトの計画，そしてゲーデルの，これら一連の歴史の結果，数学は，数学そのものとそれを今日の段階の力で記述する方法としての体系の分離と統一を見いだしたのだ．体系とは完結したものではなく，それ自体が開かれた発展する方法なのである．

次: 参考書 上: 不完全性定理 前: 形式化された数学