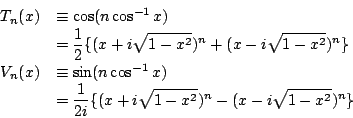
定義
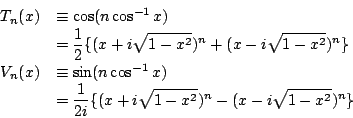
それぞれ,チェビシェフの多項式,第二種のチェビシェフの関数という.
![]() はこれまで定義してきたものと同一.
はこれまで定義してきたものと同一.
![]() は
は
![]() ,
,![]() は
次の微分方程式と漸化式の独立な解である.
は
次の微分方程式と漸化式の独立な解である.
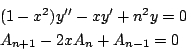
超幾何級数表示
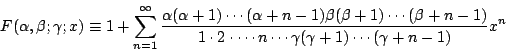
超幾何級数を用いると,チェビシェフの関数は以下のように表される.
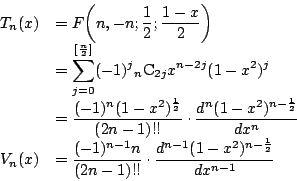
生成関数(母関数)
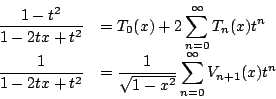
直交関係
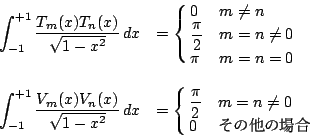
南海 この直交関係などは計算できる. このようにチェビシェフの多項式はさすがに複素数の一般的な関係から作られただけに さまざまの深い性質を持っている.
耕一 どうしてこれを「チェビシェフの多項式」 と呼ぶのですか.
南海
チェビシェフ(1821〜1894)は確率論や解析学で大きな功績のあるソビエトの数学者だ.
かれは確率論の研究の中で最高次数の係数が1の任意の![]() 次の多項式
次の多項式
![]() の
の![]() における最大偏位は
における最大偏位は
![]() より小さくなることはできない,このことを証明する必要があって,
その道具として「チェビシェフの多項式」を作り出したのだ.
より小さくなることはできない,このことを証明する必要があって,
その道具として「チェビシェフの多項式」を作り出したのだ.
耕一 そうなのですか.今日はありがとうございました.