耕介
整数の部分集合![]() で,
で,![]() の2つの元の差,
および
の2つの元の差,
および![]() の元の整数倍が再び
の元の整数倍が再び![]() に属するような
部分集合をイデアルという,とありました.
に属するような
部分集合をイデアルという,とありました.
南海
これを多項式の場合に正確に言おう.
![]() 変数の多項式の集合
変数の多項式の集合![]() には,
和の単位元 0と積の単位元 1があり,
和差および積の演算で閉じている,
つまりそれらの演算の結果は再び
には,
和の単位元 0と積の単位元 1があり,
和差および積の演算で閉じている,
つまりそれらの演算の結果は再び![]() に属する.
このような性質をもつ集合を環という.
多項式の集合の場合は多項式環といわれる.
に属する.
このような性質をもつ集合を環という.
多項式の集合の場合は多項式環といわれる.
例えば,
1変数多項式環![]() で定数項が0であるような多項式の集合
で定数項が0であるような多項式の集合![]() はイデアルである.
はイデアルである.
さて,イデアル![]() が
が
![]() で生成されるとは,
で生成されるとは,
![]() の各元
の各元![]() が
が
![]() の中の
(
の中の
(![]() によって異なってもよい)有限個の
によって異なってもよい)有限個の
![]() を用いて
を用いて
![]() と書き表されることをいう.いいかえると,
と書き表されることをいう.いいかえると,
耕介
![]() は
は![]() で生成されます.
で生成されます.
南海
そう.この場合は1つの元で生成される.
さて,次の基本定理が成り立つ.
つまり,上の
![]() を固定することが出来る.
を固定することが出来る.
![]() の変数の個数
の変数の個数![]() についての
数学的帰納法でおこなう.
についての
数学的帰納法でおこなう.
![]() のとき.このとき多項式環は定数項のみからなり
のとき.このとき多項式環は定数項のみからなり![]() そのものである.
そのものである.
![]() の任意のイデアル
の任意のイデアル![]() に対し,0でない
に対し,0でない![]() の元
の元![]() を取ると,
を取ると,
![]() が
が![]() の元なので,
の元なので,![]() との積1が
との積1が![]() に属する.
したがって任意の
に属する.
したがって任意の![]() の元
の元![]() に対して,
に対して,![]() より,
より,
![]() が
が![]() に属する.つまり,
に属する.つまり,![]() のイデアルは
のイデアルは![]() と
と![]() しかない.
このときは
しかない.
このときは![]() はそれぞれ0と1で生成される.
はそれぞれ0と1で生成される.
変数の個数が![]() のとき,
つまり
のとき,
つまり
![]() で定理が成立するとする.
で定理が成立するとする.
![]() の元
の元
![]() を
を![]() で整理し,
で整理し,
次に![]() に対して
に対して
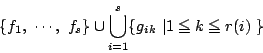
![]() を示す.
を示す.![]() は明か.
は明か.
![]() の任意の元
の任意の元![]() をとる.
をとる.
![]() を
を![]() の次数に関する数学的帰納法で示す.
の次数に関する数学的帰納法で示す.
![]() なら,
なら,![]() より成立.
より成立.
![]() 次までは成立するとする.
次までは成立するとする.
![]() のとき.
のとき.
![]() なので,
なので,
![]() の元
の元![]() を用いて
を用いて
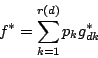
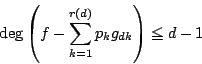
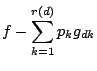 は
は
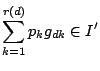 であるから,
あわせて
であるから,
あわせて
![]() のとき.
同様に考え
のとき.
同様に考え
![]() の元
の元![]() を用いて
を用いて
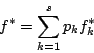
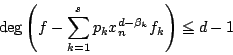
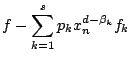 は
は
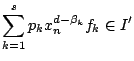 であるから
であるから
よって![]() となり,
となり,![]() が示された.
が示された.
この結果![]() が有限個の元で生成されることが確定した.
□
が有限個の元で生成されることが確定した.
□