


次: ユニタリー群の場合
上: 存在と構成
前: ヒルベルトの基底定理
南海
この基底定理を根拠にすると,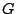 が有限群の場合,
ヒルベルトの問題が肯定的に示される.
多項式環
が有限群の場合,
ヒルベルトの問題が肯定的に示される.
多項式環![$K[{\bf x}]$](images/img479.png) の元
の元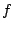 に対し
に対し
とおく.ただし,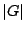 は
は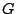 の要素の個数を表す.
の要素の個数を表す.
耕介
これって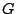 が作用していった多項式の平均ではありませんか.
が作用していった多項式の平均ではありませんか.
南海
そうだ.
補題 1
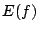 は
は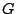 不変である.
不変である.
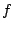 が
が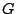 不変なら
不変なら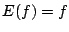 .
.
-
![$f,\ g\in K[{\bf x}]$](images/img545.png) に対し
に対し
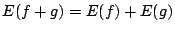 .
.
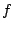 が
が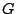 不変なら
不変なら
![$g\in K[{\bf x}]$](images/img547.png) に対し
に対し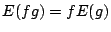 .
.
証明
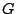 の要素を
の要素を
とし,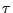 を
を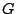 の任意の要素とすると,
の任意の要素とすると,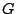 が群なので
が群なので
である.だから
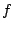 が何であっても
が何であっても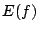 は
は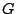 不変である.
不変である.
- 明らかである.
- 明らかである.
-
□
さらに一点注意として,
![$f\in K[{\bf x}]$](images/img553.png) への
への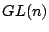 の作用は次数を変えないので,
の作用は次数を変えないので,
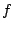 が
が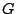 不変式なら,
不変式なら,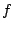 を
を
と分割すると,各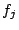 が
が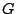 不変式である.
不変式である.
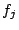 を斉次不変式という.
を斉次不変式という.
定理 8
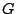
を
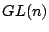
の有限部分群とし,
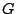
不変式の集合を
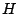
とする.
有限個の
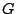
不変式

が存在し,
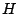
の各要素
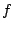
を適当な
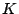
多項式
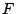
を用いて,
と表すことができる.
証明
次数が正の斉次不変式が生成する![$K[{\bf x}]$](images/img479.png) のイデアルを
のイデアルを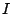 とする.
ヒルベルトの基底定理により,
とする.
ヒルベルトの基底定理により,
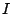 は有限個の次数正の
は有限個の次数正の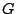 不変斉次式
不変斉次式
 で生成される.
で生成される.
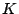 係数の
係数の
 の多項式の集合を
の多項式の集合を
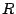 とする.
とする.
を示せばよい.
は明らかである.そこでこれが一致しないとする.
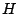 の元であって
の元であって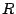 には属さない不変式が存在する.
そのような不変式の斉次部分全体のなかで,
次数が最小のものを
には属さない不変式が存在する.
そのような不変式の斉次部分全体のなかで,
次数が最小のものを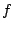 とする.
とする.
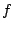 は次数最小の
は次数最小の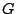 不変斉次式である.
不変斉次式である.
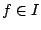 なので,斉次式
なので,斉次式
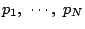 が存在して
が存在して
とかける.このとき
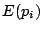 がすべて
がすべて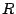 の元なら結局
の元なら結局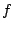 が
が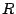 の元になる.
したがって
の元になる.
したがって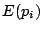 の中に
の中に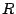 の元ではないものが存在する.
それを
の元ではないものが存在する.
それを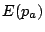 とする.
とする.
一方,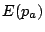 はそれ自身
はそれ自身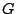 不変斉次式なので
不変斉次式なので
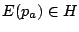 である.そして
である.そして
なので,これは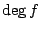 の最小性に反する.
よって
の最小性に反する.
よって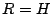 が示された.□
が示された.□
Aozora Gakuen
![]() が有限群の場合,
ヒルベルトの問題が肯定的に示される.
多項式環
が有限群の場合,
ヒルベルトの問題が肯定的に示される.
多項式環![]() の元
の元![]() に対し
に対し
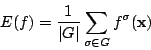
![]() が作用していった多項式の平均ではありませんか.
が作用していった多項式の平均ではありませんか.
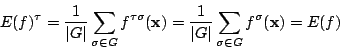
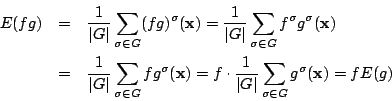
![]() への
への![]() の作用は次数を変えないので,
の作用は次数を変えないので,
![]() が
が![]() 不変式なら,
不変式なら,![]() を
を
![]() のイデアルを
のイデアルを![]() とする.
ヒルベルトの基底定理により,
とする.
ヒルベルトの基底定理により,
![]() は有限個の次数正の
は有限個の次数正の![]() 不変斉次式
不変斉次式
![]() で生成される.
で生成される.
![]() 係数の
係数の
![]() の多項式の集合を
の多項式の集合を
![]() とする.
とする.
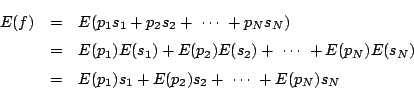
![]() はそれ自身
はそれ自身![]() 不変斉次式なので
不変斉次式なので
![]() である.そして
である.そして