耕介
有限群の場合は,総和を群の元の個数で割った平均![]() をつかうことで,
数学的帰納法がうまく使えました.
無限群では,加えたものを元の個数で割るということは出来ません.
をつかうことで,
数学的帰納法がうまく使えました.
無限群では,加えたものを元の個数で割るということは出来ません.
南海 しかし,総和に代わるものがあるだろう.
耕介 積分ですか.
南海
そうだ.全体にわたる積分が有限確定なら,
平均を考えることも不可能ではない.
そのことを話してみよう.
そこで,ここからは多項式環の係数は複素数![]() とする.
よって
とする.
よって![]() も成分は複素数値である.
も成分は複素数値である.
耕介
複素数![]() で
で![]() であるようなものによって
であるようなものによって
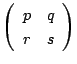 と表される行列の全体です.
しかしそうすると,
と表される行列の全体です.
しかしそうすると,![]() が作用するベクトル空間も
複素数成分ですか.
が作用するベクトル空間も
複素数成分ですか.
南海
そうだ.
![]() であるような空間を考える.
これを
であるような空間を考える.
これを![]() と書こう.
と書こう.
耕介 複素2次元ということは,実数から見れば4次元ですか.
南海
そうだ.そして,ベクトル
![]() の大きさを
の大きさを
耕介
これって2つのベクトル
![]() と
と
![]() の内積です.
の内積です.
南海
普通これを「エルミート積」という.
内積の記号を使うと
![]() と書ける.
と書ける.
![]() の元であって,
の元であって,![]() のベクトルの大きさ,
つまりエルミート積を変えないものの集合を
のベクトルの大きさ,
つまりエルミート積を変えないものの集合を![]() と書く.
これは
と書く.
これは![]() の部分群でユニタリ群といわれる.
この群は有限群とは違うが,全体を積分した値が有限である.
それを考える.
そこでまず,
の部分群でユニタリ群といわれる.
この群は有限群とは違うが,全体を積分した値が有限である.
それを考える.
そこでまず,![]() の元はどんな形をしているか.
の元はどんな形をしているか.
耕介
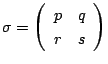 とします.また任意の
とします.また任意の
![]() をとります.
内積を1行2列,あるいは2行1列の行列の積と見れば
をとります.
内積を1行2列,あるいは2行1列の行列の積と見れば
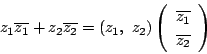
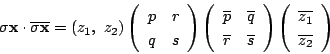
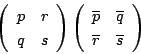
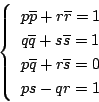
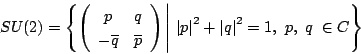
これは,実成分で
![]() とおくと
とおくと
南海
4次元空間の中の3次元球面だ.
そこで,
耕介 そんな積分はわかりません.
南海 では,円の面積と円周, 球の体積と表面積はどのような関係であったか.
耕介

南海
上段を![]() で微分すると下段になる.
球の体積は円の面積から回転体の体積計算で求まる.
で微分すると下段になる.
球の体積は円の面積から回転体の体積計算で求まる.
耕介
3次元の体積を回転させて![]() を求め,それを微分すれば
を求め,それを微分すれば![]() になるのですね.
になるのですね.
![]() を固定すると
を固定すると
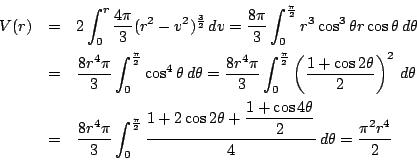
南海
とにかく有限群ではないが,![]() はその3次元球面としての総面積が
はその3次元球面としての総面積が
![]() であることがわかった.
であることがわかった.
南海
これで次の場合に不変式が有限個でかけることが示せる.
そのために![]() の不変式について
もうういちどふり返っておこう.
の不変式について
もうういちどふり返っておこう.
![]() の元
の元![]() に対して2の方法で
に対して2の方法で
![]() の
の![]() 次式が変換され,その結果
次式が変換され,その結果![]() 個の係数の間の変換が定まる.
今は,不変式の伝統に従い
個の係数の間の変換が定まる.
今は,不変式の伝統に従い
![]() を(5)において係数の変換定めている.
を(5)において係数の変換定めている.
この過程を通して![]() が
が
![]() 変数の整式に作用するのだった.
そこで
変数の整式に作用するのだった.
そこで![]() をこのような
をこのような![]() 変数の整式とし,
この作用による
変数の整式とし,
この作用による![]() の変換を
の変換を![]() と書こう.
と書こう.
今は,![]() の部分群
の部分群![]() の不変式を考えるのだ.
の不変式を考えるのだ.
耕介
有限群の場合に平均![]() をとった作用に関して,
ユニタリー群
をとった作用に関して,
ユニタリー群![]() の場合は,
形式的には
の場合は,
形式的には![]() の整式
の整式![]() に対して
に対して
南海
有限群のときは単なる和であったが,
この場合は積分なので,
![]() の元を
の元を
![]() にかけると,
これは球面
にかけると,
これは球面![]() をそれ自身に写す変換であるが,
この変換で
をそれ自身に写す変換であるが,
この変換で![]() が変わらないことをおさえなければならない.
ところが
が変わらないことをおさえなければならない.
ところが![]() はエルミート積を一定に保ち,
図形的には球面
はエルミート積を一定に保ち,
図形的には球面![]() の長さとなす角,したがってその面積要素を変えない.
この結果
の長さとなす角,したがってその面積要素を変えない.
この結果![]() は
は![]() の作用による不変式となる.
の作用による不変式となる.
![]() が
が![]() 不変なら
不変なら![]() も成り立つ.
も成り立つ.
耕介
まだ![]() 不変ではないですね.
不変ではないですね.
南海 そう.それはこれから考える.
今わかったことは,次のことだ.