南海 いいところに気づいた. 不変式の観点から対称式を考えよう. 対称式とはどんなものであったか.
耕介
2変数の場合は
![]() のように,
のように,
![]() と
と![]() を入れ替えても式が同一になるものです.
この場合
を入れ替えても式が同一になるものです.
この場合![]() を
を![]() と
と![]() の
対称式という.とくに
の
対称式という.とくに
2変数の基本対称式は,2次方程式の解と係数の関係に現れます.
つまり,
2次方程式 ![]() の解を
の解を
![]() とするとき,
とするとき,
3変数の場合は, ![]() の整式で
の整式で
![]() をどのように入れ替えても式がかわらないものを対称式という.
3変数の基本対称式は,
をどのように入れ替えても式がかわらないものを対称式という.
3変数の基本対称式は,
南海
さて,一般に![]() 個の文字変数の対称式を定義しよう.
個の文字変数の対称式を定義しよう.
![]() の
単項式で各文字に関する次数の和をその単項式の次数という.
単項式の次数の最大値を,その整式の次数という.
の
単項式で各文字に関する次数の和をその単項式の次数という.
単項式の次数の最大値を,その整式の次数という.
![]() が
が
![]() の対称式であるとは
文字変数
の対称式であるとは
文字変数
![]() のどのような置きかえに対しても,
整式が不変であることをいう.
文字の置きかえはいくつあるか.
のどのような置きかえに対しても,
整式が不変であることをいう.
文字の置きかえはいくつあるか.
耕介
![]() の並べ替えだけあります.
つまり
の並べ替えだけあります.
つまり![]() 個です.
個です.
南海
これらの置きかえも,![]() の要素で表せる.
の要素で表せる.
![]() のとき,
のとき,
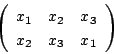
耕介
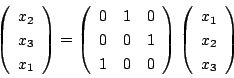
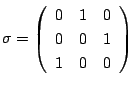 が対応します.
が対応します.
![]() 変数でも,変数の置換は
各行各列の一カ所ずつのみが1で後は0の
変数でも,変数の置換は
各行各列の一カ所ずつのみが1で後は0の![]() 次行列で表せる.
それが
次行列で表せる.
それが![]() 個ある.
個ある.
南海
つまり,![]() 個の文字の置きかえは,
要素の個数が
個の文字の置きかえは,
要素の個数が![]() 個の
個の![]() の部分群になる.
普通これを
の部分群になる.
普通これを![]() 等と表し,
等と表し,![]() 次対称群という.
次対称群という.
耕介
そうか.
対称式とは対称群![]() に関する不変式なのですね.
に関する不変式なのですね.





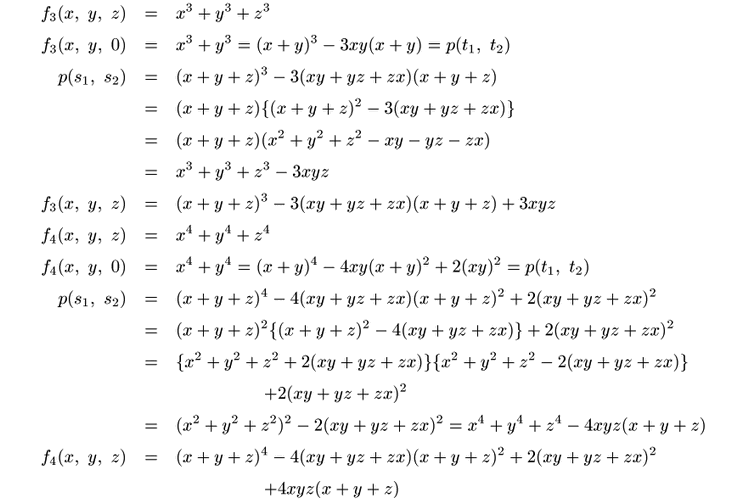
南海
この証明は,![]() 次方程式には
次方程式には![]() 個の根が存在するという,
代数学の基本定理を用いた.
基本定理を用いないで,計算だけで示すこともできる.
また考えてみておいてほしい.
個の根が存在するという,
代数学の基本定理を用いた.
基本定理を用いないで,計算だけで示すこともできる.
また考えてみておいてほしい.
この定理の系として,次のことが示される. なお, 系というのは, 定理からただちに本質的な証明を経ずに得られる結果をいう.
証明
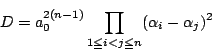
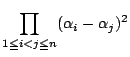 は
明らかに
は
明らかに
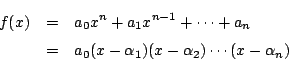
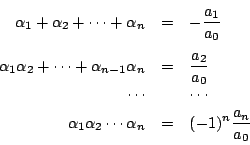
定理2によって,
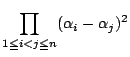 は
は
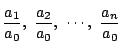 の
の![]() 次式で表され,
次式で表され,
![]() は係数
は係数
![]() の
の![]() 次の整式である.
次の整式である.
![]() が係数
が係数
![]() の整式として
の整式として
![]() と因数分解されたとする.
ところが,
と因数分解されたとする.
ところが,![]() も
も![]() も
も
![]() の整式ということは,
の整式ということは,
![]() の対称式ということである.
の対称式ということである.
![]() を
を![]() の整式と見れば
の整式と見れば![]() に
に![]() を代入すれば0になるので,
このとき,
を代入すれば0になるので,
このとき,![]() か
か![]() のいずれかが0である.
のいずれかが0である.
![]() とすれば
とすれば![]() は
は
![]() を因数にもち,
を因数にもち,
![]() はもたない.
はもたない.
![]() とすれば
とすれば
![]() は
は
![]() を因数にもつ.
を因数にもつ.
対称性から第一の場合は,![]() が
が
![]() と因数をすべてもち
と因数をすべてもち![]() が定数である.
つまり
が定数である.
つまり![]() は
は![]() のべきであるが,
これは
のべきであるが,
これは![]() が
が![]() を因数にもつことを示している.
ところが
を因数にもつことを示している.
ところが![]() は
は
![]() の定数倍で,
これは
の定数倍で,
これは
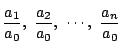 の
の![]() 次式であるから,
次式であるから,
![]() は
は
![]() の整式として
の整式として![]() を因数にもつことはあり得ない.
を因数にもつことはあり得ない.
第二の場合は![]() がともに
がともに
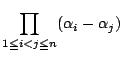 を因数にもつが,これは
を因数にもつが,これは![]() の対称式ではない.
□
の対称式ではない.
□
を2変数
に関する実数を係数にもつ多項式とする.
とおく. このとき, 以下の問いに答えよ.