- 2次式
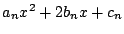 の判別式を
の判別式を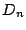 とする.
とする.
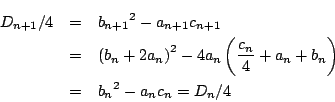
よって帰納的に
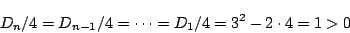
したがって, 2次方程式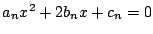 は相異なる2次数解をもち,
は相異なる2次数解をもち,
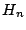 は
は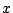 軸と2点で交わることが示された.
軸と2点で交わることが示された.
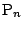 ,
,
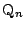 の
の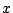 座標を
座標を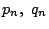 とする.
とする.
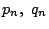 は2次方程式
は2次方程式
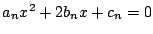 の2解であるから,
の2解であるから,
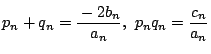 である.
よって
である.
よって
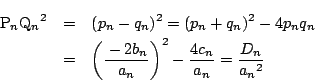
(1)から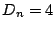 なので
なので
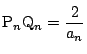 である.
ここで条件から
である.
ここで条件から
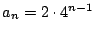 であるから,
であるから,
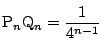 である.
である.
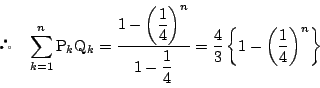
別解
-
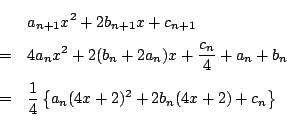
したがって2次方程式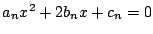 の解を
の解を
 とすれば,
2次方程式
とすれば,
2次方程式
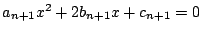 の解は
の解は
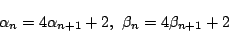
となる.これから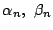 が異なる実数なら,
が異なる実数なら,
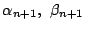 も異なる実数である.
も異なる実数である.
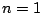 のときは
のときは
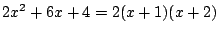 より
より
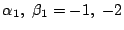 .
数学的帰納法によって,
2次方程式
.
数学的帰納法によって,
2次方程式
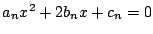 は相異なる2次数解をもち,
は相異なる2次数解をもち,
 は
は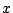 軸と2点で交わることが示された.
軸と2点で交わることが示された.
-
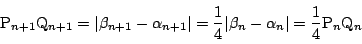
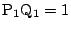 なので
なので
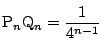 である.
である.
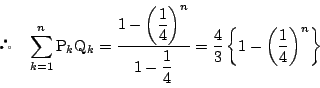
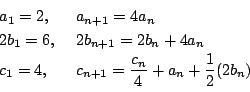
とすると,2次式の係数変換行列が
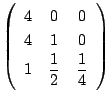 となる.これが変換4となるように
となる.これが変換4となるように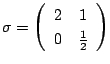 となる.別解はこのことを背景に用いている.
となる.別解はこのことを背景に用いている.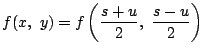 より,
より,
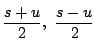 の多項式となるから
の多項式となるから
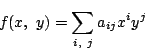
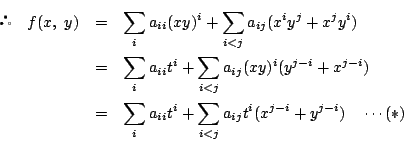

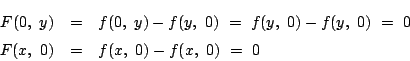
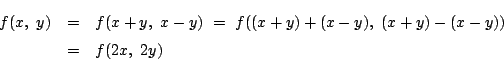
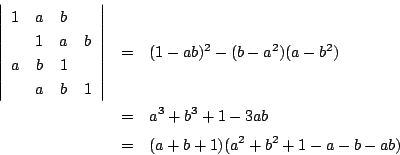
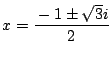 .
.
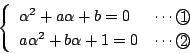
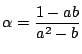 が必要である.
これから
が必要である.
これから
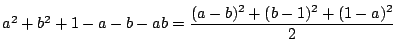 より,
係数実数でこれが0になるのは
より,
係数実数でこれが0になるのは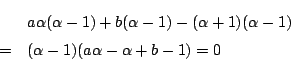
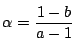 が必要.
が必要.
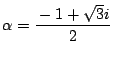 または
または
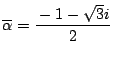 .
係数が実数なので一方が共通解なら他方も共通解である.
.
係数が実数なので一方が共通解なら他方も共通解である.