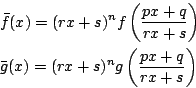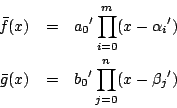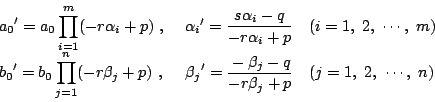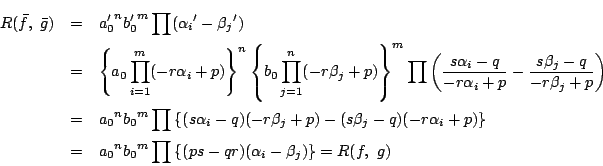次: 終結式の行列式表現
上: 判別式と終結式
前: 終結式と判別式
また,判別式の場合と同様に,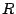 は
は
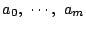 および
および
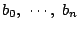 の整式として,既約である.
さて,終結式もまた不変式であることを確認しよう.
不変性の確認なので等式2によって定まる
の整式として,既約である.
さて,終結式もまた不変式であることを確認しよう.
不変性の確認なので等式2によって定まる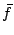 ,
および同様にして定まる
,
および同様にして定まる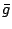 に関して示せばよい.
に関して示せばよい.
定理 4
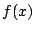
と
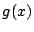
はそれぞれ
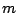
次,
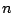
次の整式で最高次数の項の係数は
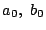
であるとする.
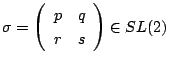
に対し
で
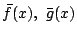
を定めるこのとき,
である.
証明
判別式の証明で示したように
とすると,
となる.だから
となる.
Aozora Gakuen
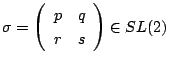 に対し
に対し
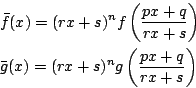
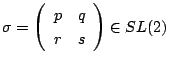 に対し
に対し