次: 四次方程式の一般的解法(2)
上: 4次方程式
前: 別のb の値なら?
耕一
この方法はそのまま文字にしてもできます.
一般の四次方程式
は
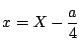 とすると X の三次の項が消える.
とすると X の三次の項が消える.
したがって,はじめから
としてよい.このとき
となるようにする.
これから 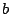 の三次方程式
の三次方程式
を得る.この 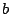 の値を三次方程式の解を求める方法によって定める.
の値を三次方程式の解を求める方法によって定める.
それによって定める二つの二次方程式
から,四次方程式の四つの根が求まる.
ただし
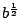 は2乗すれば
は2乗すれば 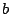 となる二つの複素数の一方を表す.
となる二つの複素数の一方を表す.
南海
よくまとまっている.
これが「フェラーリ(Lodovico Ferrari 1552〜1565)の方法」よ呼ばれるものである.
Aozora Gakuen
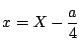 とすると X の三次の項が消える.
とすると X の三次の項が消える.