


次: ガロアの生涯
上: 4次方程式
前: 四次方程式の一般的解法(1)
耕一
三次方程式のときのように,
一次式の積に分解される四次式を使う解法はないのでしょうか.
南海 それがあるのだ.次の式を展開してほしい.
耕一 やってみます.
これを 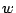 で整理すると
で整理すると
これが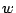 の4次式として,xの4次式
の4次式として,xの4次式
と一致するように決められれば,解が得られる つまり
これから
これを第3式に代入すると
これから 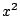 の三次方程式
の三次方程式
が得られる.
つまり三次方程式と平方根で 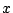 が得られ,
が得られ, 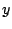 と
と 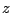 は二次方程式で得られて,
もとの四次方程式が解ける!
は二次方程式で得られて,
もとの四次方程式が解ける!
南海 というわけだ.このように四次方程式も
係数に関する「根号」演算と四則演算で解ける.
Aozora Gakuen
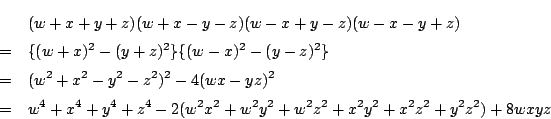
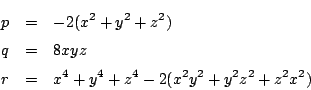
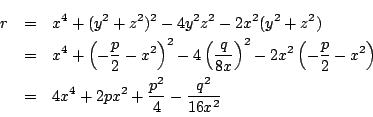
![]() が得られ,
が得られ, ![]() と
と ![]() は二次方程式で得られて,
もとの四次方程式が解ける!
は二次方程式で得られて,
もとの四次方程式が解ける!