証明
![]() を
を ![]() で割った商を
で割った商を ![]() ,余りを
,余りを ![]() とする.
とする.
ここで ![]() と
と ![]() を
を ![]() と
と ![]() で表す.
で表す.
まず
![]() .次に
等式1.1の両辺を
.次に
等式1.1の両辺を ![]() で微分する.
で微分する.
したがって
![]() で割った余りは
で割った余りは
したがって,条件
耕一
![]() を
を![]() で割った余りは1次式で,それはちょうど
で割った余りは1次式で,それはちょうど ![]() の
の
![]() での接線の式になるのだ.
での接線の式になるのだ.
南海 当然ではあるが,出てきた結果を解釈し感心するというのは数学にとっては大切なことだ.
耕一
でも最初に戻って,この例題では,
与えられた![]() が重根かどうかを判断することはできても,
が重根かどうかを判断することはできても, ![]() が重根をもつかどうかは,わかりません.
が重根をもつかどうかは,わかりません.
南海
その通りだ.
しかし,この例題から![]() が重根
が重根 ![]() をもつならそれは
をもつならそれは ![]() の根でもある.
だから,
の根でもある.
だから, ![]() の重根
の重根 ![]() は
は ![]() と
と ![]() の共通因数を
の共通因数を ![]() と
するとき,
と
するとき, ![]() の根であることがわかる.
の根であることがわかる.
![]() と
と ![]() が定数でない共通因数
が定数でない共通因数 ![]() をもつかどうかは判断できるではないか.
をもつかどうかは判断できるではないか.
![]() と
と ![]() の共通因数 ,つまり
の共通因数 ,つまり![]() と
と ![]() の公約数を見つける一般的な方法が
ユークリッドの互除法である.
の公約数を見つける一般的な方法が
ユークリッドの互除法である.
耕一
そうか. ![]() と
と ![]() が互いに素なら
が互いに素なら ![]() に重根はなく,あるとすれば
それは
に重根はなく,あるとすれば
それは ![]() と
と ![]() の公約数を
の公約数を ![]() とするとき,
とするとき, ![]() の根だ.
そして公約数
の根だ.
そして公約数 ![]() はユークリッドの互除法で求まる.
それで重根をもつかどうかが判断できる.
はユークリッドの互除法で求まる.
それで重根をもつかどうかが判断できる.
南海
ちなみに
耕一
![]() とします.
とします.
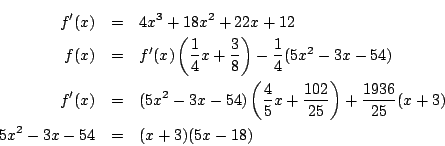
したがって ![]() と
と ![]() は公約数
は公約数 ![]() をもちます.実際
をもちます.実際
南海
もちろん ![]() を見つければ因数分解はできるのだが,
このような計算を一度やっておくことは大切だ.上の互除法で
を見つければ因数分解はできるのだが,
このような計算を一度やっておくことは大切だ.上の互除法で 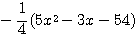 で割らずに,
で割らずに, ![]() で割ったところが重要だ.
ユークリッドの互除法で式の公約数を求める場合,定数倍だけ違うどれを余りとして
用いても同じことになる.
で割ったところが重要だ.
ユークリッドの互除法で式の公約数を求める場合,定数倍だけ違うどれを余りとして
用いても同じことになる.
耕一
式の因数分解は
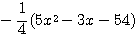 で割っても,
で割っても,