とおく.このとき方程式
の実数根はすべて区間
すべての根の絶対値がある範囲を超えないとき,その範囲を根の限界と呼ぶ. 一つの限界の定め方として次のものがある.
耕一
証明は背理法ですね. ![]() とする.
(いろいろやってみるが)しかし難しいです.
とする.
(いろいろやってみるが)しかし難しいです.
南海
2つの複素数 ![]() と
と ![]() に関して
に関して
これを使う.さらに
![]() なので
なので
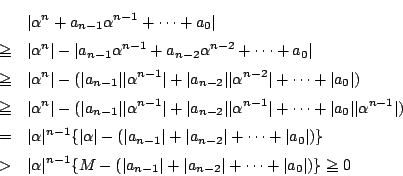
しかし,この ![]() は係数の絶対値の和なので結構大きい.もう少し小さい限界がとれる.
同様の論証で次の定理が成り立つ.
は係数の絶対値の和なので結構大きい.もう少し小さい限界がとれる.
同様の論証で次の定理が成り立つ.
証明
![]() のとき.(1.2)は
のとき.(1.2)は
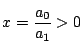 は確かにただ一つの正の解である.
は確かにただ一つの正の解である.
![]() のとき成立するとする.
のとき成立するとする.
![]() のとき.
のとき.
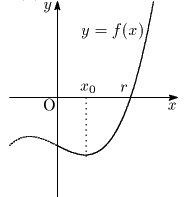 ここで係数
ここで係数
それを ![]() とする.
とする. ![]() なので
なので ![]() は
は ![]() で負から正に変わる.
つまり
で負から正に変わる.
つまり ![]() は
は ![]() で極小である.
で極小である.
![]() なので
なので ![]() はただ一つ正の解
はただ一つ正の解 ![]() をもつ.
をもつ.
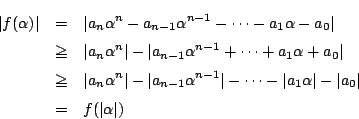
したがって ![]() である複素数
である複素数 ![]() に対しては(1)から
に対しては(1)から
![]() なので
なので![]() となることはあり得ない.
となることはあり得ない.
よって(1.2)の他の解 ![]() はすべて
はすべて ![]() をみたす.□
をみたす.□
この前半(1)は数学的帰納法の演習問題だ.この定理を生かすと根の限界について もう少し小さい値を取ることができる.
証明
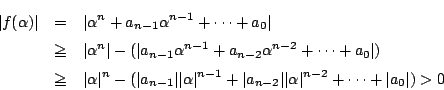
一般に,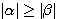 である複素数
である複素数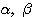 に関する三角不等式
に関する三角不等式
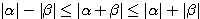
において,左の等号が成立するのは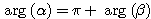 のとき,右の等号が成立するのは
のとき,右の等号が成立するのは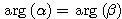 のときである.ただし偏角は0から
のときである.ただし偏角は0から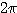 にとるものとする.
にとるものとする.
つまり![]() となる
となる ![]() が解であり得るのは,上の二つの複素数に関する
不等式で等号が成り立つときである.つまり
が解であり得るのは,上の二つの複素数に関する
不等式で等号が成り立つときである.つまり
今,
![]() とおくと
とおくと
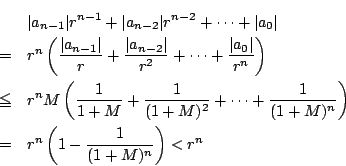
ゆえに解 ![]() に対しては
に対しては ![]() である.□
である.□
証明
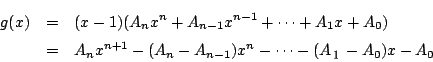
この係数
![]() は
は ![]() を解にもつので,定理1(2)から
を解にもつので,定理1(2)から ![]() の
の ![]() 以外の
解
以外の
解 ![]() はすべて
はすべて ![]() をみたす.つまり
をみたす.つまり
![]() となる解があるとする.
となる解があるとする. ![]() の偏角を
の偏角を ![]() とする.偏角を
とする.偏角を ![]() で考える.
で考える.
![]() となるのは
定理1の(2)の証明で2つの不等式でともに等号が成立するときなので,
となるのは
定理1の(2)の証明で2つの不等式でともに等号が成立するときなので,
ところが ![]() のとき
のとき
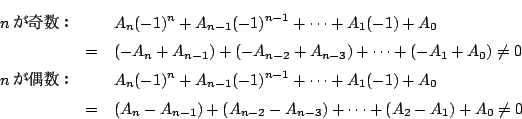
南海 このような根の限界は他にもいろいろとある.ただそれは今日の主題ではないのでここでおく.