![]() を実係数をもつ
を実係数をもつ ![]() 次多項式
次多項式
以下, ![]() の零点
の零点 ![]() とは
とは ![]() となる実数
となる実数 ![]() のこととする.
のこととする.
![]() と
と ![]() に対してユークリッドの互除法を行う.
そのとき余りを次の定理のなかで述べられているように,通常の場合と符号を逆にとる.
に対してユークリッドの互除法を行う.
そのとき余りを次の定理のなかで述べられているように,通常の場合と符号を逆にとる.

![]() の零点でない実数
の零点でない実数 ![]() に対して,数の列
に対して,数の列
![]() は
は ![]() の零点でないとする.このとき区間
の零点でないとする.このとき区間 ![]() 内の
相異なる零点の個数(したがって重根も1つと数える)は
内の
相異なる零点の個数(したがって重根も1つと数える)は
南海
ユークリッドの互除法により,
![]() は
は![]() と
と ![]() の最大公約数である.
これが互いに素,つまり
の最大公約数である.
これが互いに素,つまり ![]() が重根をもたなければ,
が重根をもたなければ, ![]() は定数である.
は定数である.
耕一
この種の問題を考えるのに ![]() と
と ![]() は必要だとわかります.
しかしそのあと,順に
は必要だとわかります.
しかしそのあと,順に
![]() と作っていってそれを調べるのかな,と
思っていたのですが,互除法で次々に決めていくのですね.
と作っていってそれを調べるのかな,と
思っていたのですが,互除法で次々に決めていくのですね.
南海 スツルムの時代,いろんな試行錯誤があったのだろう. 当然,高次微分との関係も調べられたに違いない.
高次微分の列
高次微分は
![]() の3項の間の関係を
数式で表わしにくい.が,互除法ならはっきりしている.
さらに互除法で余りの符号を逆にとるなどということは,ほんとにいろんな工夫の後に,
スツルムにひらめいたのだ.こうして任意の区間内の実根の個数を確定するという問題を
スツルムが最初に解決した.
の3項の間の関係を
数式で表わしにくい.が,互除法ならはっきりしている.
さらに互除法で余りの符号を逆にとるなどということは,ほんとにいろんな工夫の後に,
スツルムにひらめいたのだ.こうして任意の区間内の実根の個数を確定するという問題を
スツルムが最初に解決した.
証明
![]() が重根をもたない場合.
が重根をもたない場合.
この場合, ![]() と
と ![]() は互いに素なので,
は互いに素なので, ![]() は0でない定数で,
隣りあう2項の零点に同じものはない.
は0でない定数で,
隣りあう2項の零点に同じものはない.
区間 ![]() で
で ![]() を固定し
を固定し ![]() を動かすことを考える.
を動かすことを考える.
区間内の実数![]() で
で![]() の零点ではないものをとる.
この
の零点ではないものをとる.
この![]() に対し,
に対し,![]() を零点にもつ
を零点にもつ![]() で,
で,![]() にあるものをとる.
にあるものをとる.
![]() を
を
![]() で区間
で区間 ![]() に
に
![]() 以外の
以外の![]() の零点が存在しないようにとる.
の零点が存在しないようにとる.
このとき
![]() である.
である.
このような![]() が存在しなければ,すべて符号が一定なので明らかである.
が存在しなければ,すべて符号が一定なので明らかである.
存在するときを考える.
![]() の前後の
の前後の
![]() は
は ![]() を零点にはしないので
を零点にはしないので
![]() で同じ符号をとる.
で同じ符号をとる.
![]() は
は ![]() の前後で負から正に変わるとする.
の前後で負から正に変わるとする.
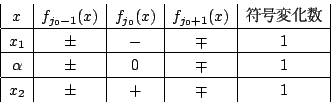
正から負に変わるときも同様である. したがって符号変化の回数は変わらない.
![]() を零点にもつ各
を零点にもつ各![]() についていえるので,
についていえるので,
![]() である.
である.
次に ![]() を
を ![]() の零点とし,同様の考察を行う.
の零点とし,同様の考察を行う.
![]() の前後で
の前後で ![]() が負から正に変わるとすると
が負から正に変わるとすると ![]() なので
なので
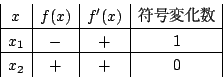

![]() を零点にもつ,
を零点にもつ,![]() の範囲の
の範囲の![]() については,先の考察と同様に
については,先の考察と同様に![]() の
前後での符号変化の回数は変わらない.
の
前後での符号変化の回数は変わらない.
よってこの場合
![]() である.
である.
したがって ![]() は
は ![]() が
が ![]() から増加して
から増加して ![]() の零点を一つ超えるごとに1増加する.
の零点を一つ超えるごとに1増加する.
つまり ![]() は区間
は区間 ![]() における
における ![]() の零点の個数そのものである.
の零点の個数そのものである.
![]() が実数の重根
が実数の重根 ![]() をもつ場合.
をもつ場合.
![]() とおく.
とおく.
![]() から
から ![]() のすべてを
のすべてを
![]() で割る.
で割る.
それをあらためて
この新たな
![]() の
の![]() での符号は,
もとの
での符号は,
もとの
![]() の
の![]() での符号と,
での符号と,
![]() の正負に
よってすべて同符号かすべて異符号かのいずれかであるから,符号変化の回数は変わらない.
の正負に
よってすべて同符号かすべて異符号かのいずれかであるから,符号変化の回数は変わらない.
新たな
![]() は隣りあう2項の間に共通の零点をもたないので
は隣りあう2項の間に共通の零点をもたないので
![]() に対する
に対する![]() の零点
の零点![]() の前後で
の前後で ![]() の値が変わらないことは
同様である.
の値が変わらないことは
同様である.
![]() を
を ![]() の零点とする.
の零点とする.
![]() なら
なら
![]() の前後で
の前後で ![]() の値が1減ることも同様である.
の値が1減ることも同様である.
最後に ![]() の前後でも
の前後でも ![]() の値が1減ることを確認する.
の値が1減ることを確認する.
![]() で
で ![]() である.
である.
今 ![]() の前後で
の前後で ![]() とし,上と同様の考察をする.
とし,上と同様の考察をする.
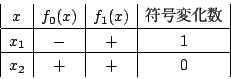
したがってこの場合も
![]() である.
である.
よって重根をもつ場合も
![]() は
は ![]() が
が ![]() から増加して
から増加して ![]() の零点を一つ超えるごとに1増加する.
の零点を一つ超えるごとに1増加する.
つまり ![]() は区間
は区間 ![]() における
における ![]() の零点の個数そのものである.
ただし,重根も1つに数えている.
の零点の個数そのものである.
ただし,重根も1つに数えている.
以上で題意が示された.□
南海
ここで大切な注意がある.区間 ![]() での符号変化回数の差
での符号変化回数の差 ![]() を求めようとするとき,ある
を求めようとするとき,ある ![]() が区間
が区間 ![]() で符号が一定になったとする.
で符号が一定になったとする.
すると ![]() の間の
の間の![]() に対し,各
に対し,各![]() が途中で符号を変えても,
すでに見たようにその前後の
が途中で符号を変えても,
すでに見たようにその前後の ![]() と
と![]() で
で ![]() の値が変わらず,
したがって区間
の値が変わらず,
したがって区間 ![]() に属する任意の
に属する任意の ![]() に対し数列
に対し数列
したがって ![]() を求めようとすれば
を求めようとすれば
さて,![]() 次方程式
次方程式 ![]() がいくつ実数解をもつかを知りたければ,
まず先に見たように,根の限界を何らかの方法で見つけそれを
がいくつ実数解をもつかを知りたければ,
まず先に見たように,根の限界を何らかの方法で見つけそれを ![]() とする.
すべての実根は区間
とする.
すべての実根は区間 ![]() にあるので
にあるので 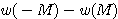 が実根の個数である.
が実根の個数である.
このようにスツルムの定理と根の限界の定理を組み合わせれば,すべての実根の 個数がわかる.
そこで最初の阪大の問題だが,スツルムの定理の簡単な応用になっていることは わかるだろうか.
耕一
![]() とすれば
とすれば
![]() .十分大きい
.十分大きい ![]() をとり
区間
をとり
区間 ![]() をとる.この区間で
をとる.この区間で![]() の符号は一定(つねに正)なので,
先の注意により
の符号は一定(つねに正)なので,
先の注意により ![]() と
と ![]() の符号変化のみを調べればよい.
の符号変化のみを調べればよい.
![]() なら
なら 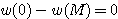 .
. ![]() なら
なら 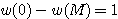 .
.
![]() のとき….
のとき….
南海
![]() のとき,つまり
のとき,つまり ![]() のときは,
任意の正の
のときは,
任意の正の ![]() に対して
に対して ![]() だから
だから 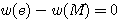 .ゆえにやはり正の解はない.
.ゆえにやはり正の解はない.
南海 区間の中に1つあることがわかれば,区間を中点で区切り調べれば,そのいずれにあるか わかる.同様にくり返せばいくらでも根の近似値を求めることができる.