- 係数の最大値は3,ゆえに根は
![$[-4,\ 4]$](images/img764.png) にある.まずこの範囲で調べ
順次範囲を狭くする.
にある.まずこの範囲で調べ
順次範囲を狭くする.
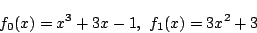
つねに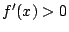 なので
なので  以下は必要ない.
以下は必要ない.
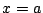 での
での 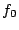 と
と 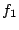 での符号変化を
での符号変化を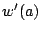 と書く.
と書く.
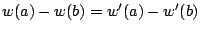 である.
である.
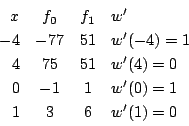
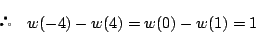
実根は1つで,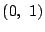 にある.
にある.
- 同様に
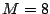 なので
なので ![$[-9,\ 9]$](images/img776.png) で調べる.
で調べる.
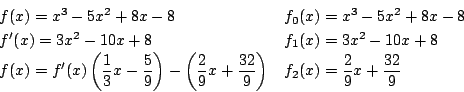
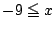 でつねに
でつねに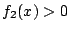 なので
なので 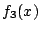 以下は必要ない.
以下は必要ない.
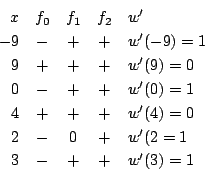
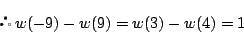
実根は1つで,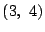 にある.
にある.
-
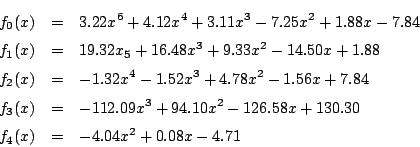
実数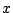 に対して
に対して 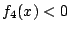 なので,以下は必要ない.計算結果を符号で書く.
なので,以下は必要ない.計算結果を符号で書く.
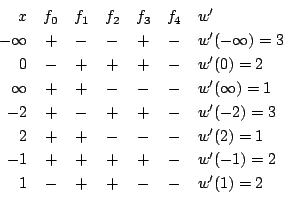
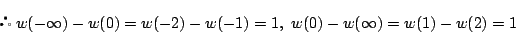
実根は2つで,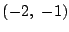 と
と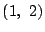 にある.
にある.
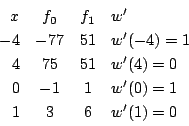
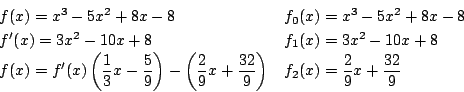
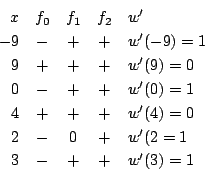
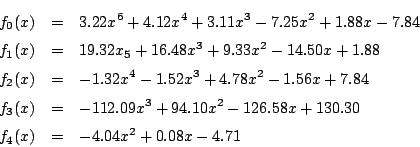
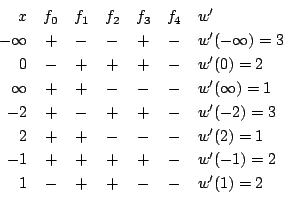
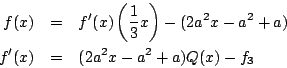
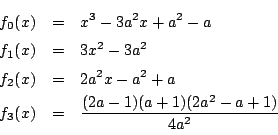
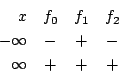
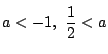
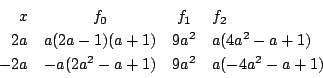
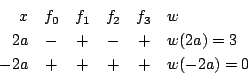
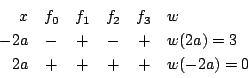
注 普通の受験参考書の解答と比較してみてほしい.
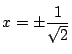 で極小となる.
で極小となる.
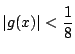 であるから,
であるから,
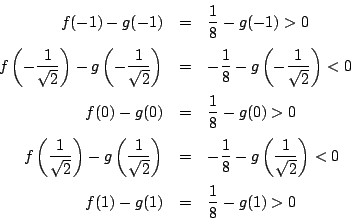
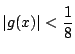 と仮定する.
と仮定する.
(2)より,![]() は少なくとも四つの解をもつ.ところが,
は少なくとも四つの解をもつ.ところが,![]() が
三次式となるので,恒等式の原理によって
が
三次式となるので,恒等式の原理によって![]() は恒等的に
は恒等的に![]() になる.つま
り
になる.つま
り![]() となり,
となり,
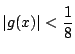 が成立しなくなる.
が成立しなくなる.
したがって,![]() は
は![]() の少なくとも一つの値で
の少なくとも一つの値で![]() 以上の値をとるので,
以上の値をとるので,![]() の最大値は
の最大値は![]() 以上である.
以上である.
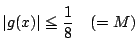 かつ,ある
かつ,ある
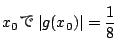 となるとする.
となるとする.
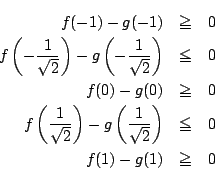
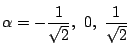 のいずれか
で同じものであったとする.
のいずれか
で同じものであったとする.
![]() より,
より,
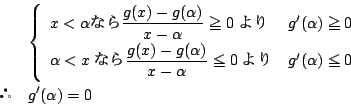
つまり![]() は
は![]() で重解となる.
で重解となる.
重複度まであわせると![]() は四つの解をもつ.
は四つの解をもつ.
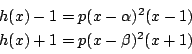
係数を比較して,
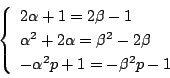
![]() で
で ![]() となる解はない.つまり
となる解はない.つまり ![]() と
と ![]() のグラフは
のグラフは
![]() では交わらない.
では交わらない.![]() より
より ![]() で.
で.![]() .
.
![]() より
より ![]() で.
で.![]() .
.
ところが ![]() のかわりに
のかわりに ![]() も同じ条件を満たすので
も同じ条件を満たすので
![]() で.
で.![]() .
.![]() で.
で.![]() .
も成り立つ.
.
も成り立つ.
ゆえに ![]() で
で
![]() が成り立ち,
が成り立ち,
![]() なる任意の実数
なる任意の実数 ![]() に対して不等式
に対して不等式
![]() を消去すると
を消去すると
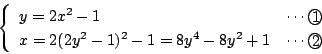
注意 これが四次のチェビシェフの多項式そのものであることに注目!!
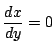 となるのは,
となるのは,
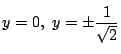 のとき.
のとき.
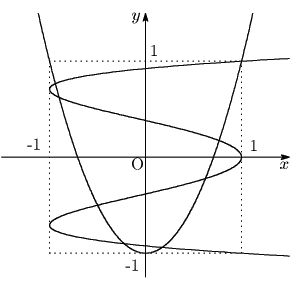
1は,
そのグラフは極と極の間の単調性によって図1のように8個の交点を持つ.
さらに![]() も消去すると
も消去すると![]() の8次方程式となるのでこれがすべての交点である.
の8次方程式となるのでこれがすべての交点である.
明らかにこれらの交点は
![]() にあるので,
にあるので,
全部で8個の解を持つことは, 既に示した.
よって(1)(2)が示された.
別解
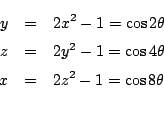
 したがって,連立方程式
したがって,連立方程式![]() の解は
の解は