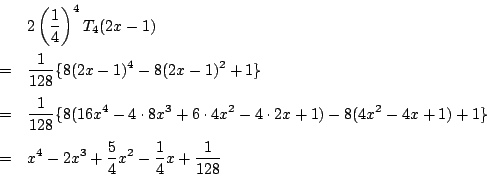次: チェビシェフの多項式の係数
上: チェビシェフの多項式
前: チェビシェフの多項式
南海
関数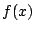 の定義域の部分集合
の定義域の部分集合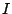 がある.
関数
がある.
関数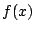 の絶対値
の絶対値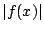 の
の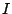 における最大値が存在するとき,
その値を
における最大値が存在するとき,
その値を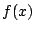 の
の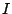 における最大偏位という.
前の問題を前提として次の問題をやってみよう.
における最大偏位という.
前の問題を前提として次の問題をやってみよう.
南海
どうかな.
耕一
(1)の後半,
「かぎり」のところが難しいです.普通に交わるときは多項式として一致するのですが,
極で重なる場合が厳密ではありません.
南海 熊本大の(4)の部分だな.少し手助けしよう.
証明
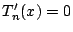 である各点での
である各点での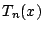 の値を調べる.
の値を調べる.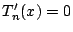 をみたす
をみたす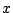 は
は
であった. この各値
に対して,
 したがって,
したがって, 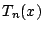 は
は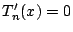 である
である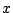 において,
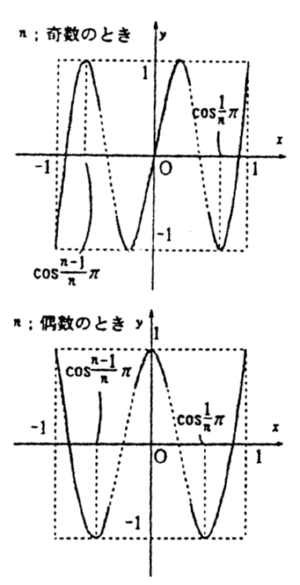
において, 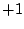 と
と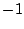 を
交互にとる. また,
を
交互にとる. また, 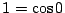 であるから,
であるから,
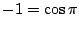 であるから,
であるから,
したがって, 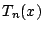 のグラフは右図のようになっている.
のグラフは右図のようになっている.
さて,
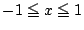 において
において
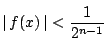 と仮定する. いま
と仮定する. いま
とおくと,
というように,
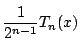 が
が
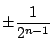 の値
をとる1から
の値
をとる1から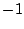 までの
までの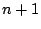 個の点で符号が入れ替わる. よって,
個の点で符号が入れ替わる. よって, 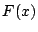 は
は
の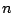 個の各区間において値 0 をとるような
個の各区間において値 0 をとるような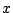 が少なくとも一つずつ存在する.
つまり,
が少なくとも一つずつ存在する.
つまり, 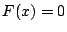 は
は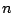 個以上の解をもつ. ところが,
個以上の解をもつ. ところが, 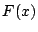 は
は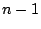 次
の多項式であるから,
次
の多項式であるから, 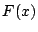 は恒等的に 0 となる. つまり,
は恒等的に 0 となる. つまり,
これは
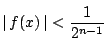 に矛盾する. したがって,
に矛盾する. したがって,
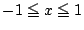 において
において
となる点が必ずあり, 最大偏位は
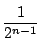 以上となる.
以上となる.
次に, もし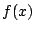 の
の
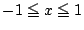 における最大偏位がちょうど
における最大偏位がちょうど
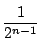 であれば,
であれば,
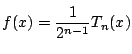 とな
ることを示す. そのために, 上と同じく
とな
ることを示す. そのために, 上と同じく
を考える. ここで, 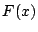 は
は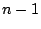 次式である. いま,
次式である. いま, 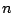 個の各区間
個の各区間
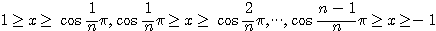
において, 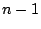 次方程式
次方程式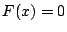 は少なくとも一つの解をもつ. その二つの解
が隣り合う二つの区間の境界点
は少なくとも一つの解をもつ. その二つの解
が隣り合う二つの区間の境界点
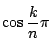 で一致したときを考える.
で一致したときを考える.
とする.
より
一方
なので
のときも同様にして
となる.
したがって,
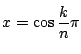 は方程式
は方程式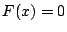 の2重以上の重解となる.
これより, 重解を含めて
の2重以上の重解となる.
これより, 重解を含めて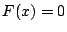 は
は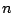 個以上の解を有することになり, こ
れは
個以上の解を有することになり, こ
れは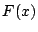 が
が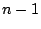 次式であることに矛盾する. よって,
次式であることに矛盾する. よって, 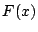 は恒等的に0であり,
は恒等的に0であり,
となる.
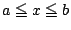 の範囲の
の範囲の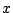 を
を
とおく. このとき,
となるので,
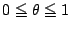 のとき
のとき
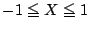 である. よって, 求める
ものは
である. よって, 求める
ものは
をその最高次の項の係数で割って 1 としたものである. ここで, 明らかに
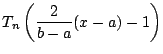 の最高次の項の係数は
の最高次の項の係数は
であるから, 求めるものは,
である.
- 最高次の項の係数が1である多項式で, 区間
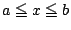 における最大偏位が
最小なものは(2)で求めたものであり, その最大偏位は
における最大偏位が
最小なものは(2)で求めたものであり, その最大偏位は
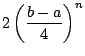 であった. よって,
であった. よって,
のときにかぎり, 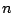 を大きくとればいくらでも小さくできるので,
を大きくとればいくらでも小さくできるので, 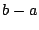 が4
より小さいことが必要十分条件である.
が4
より小さいことが必要十分条件である.
注意
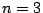 では
では
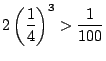 なので
不可能であるが,
なので
不可能であるが, 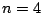 では最大偏位が
では最大偏位が
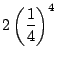 と
と
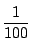 の間にくる他の四次式をつくることも可能である(たとえば,
の間にくる他の四次式をつくることも可能である(たとえば, 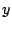 軸
方向の平行移動で). 解答で考えたのはその中で最大偏位が最小のものである.
軸
方向の平行移動で). 解答で考えたのはその中で最大偏位が最小のものである.
例 1.6.4
最高次数の項の係数が
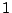
である多項式で,かつ
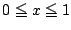
での
最大偏位が
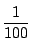
以下となるもののうち最も次数の小さいものを求めよう.
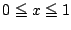 で最大偏位が最小となる最高次の項の係数が 1 である多項式は,
(2)において
で最大偏位が最小となる最高次の項の係数が 1 である多項式は,
(2)において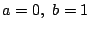 を代入して,
を代入して,
で, その最大偏位は
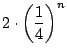
である. すると,
よって,
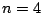
が最も次数が低い. ゆえに,
これが求める多項式である.



次: チェビシェフの多項式の係数
上: チェビシェフの多項式
前: チェビシェフの多項式
Aozora Gakuen
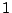 である
である 次の多項式
次の多項式
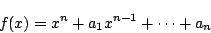
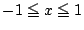 における最大偏位は
における最大偏位は
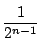 より小さくなることは
できず,
より小さくなることは
できず,
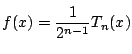 のときにかぎり,
のときにかぎり,
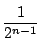 と
なる.
と
なる.
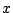 に対し,
に対し,
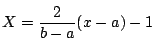 を対応させると,区間
を対応させると,区間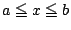 は区間
は区間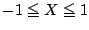 にうつる.これを用いて,最高次数の項の係数が
にうつる.これを用いて,最高次数の項の係数が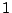 である
である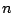 次の多項式で区間
次の多項式で区間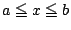 における最大偏位が最小となるものを,
における最大偏位が最小となるものを,
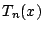 を用いて表わせる.
を用いて表わせる.
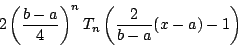
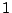 である多項式が常に作れるためには,その区間の長さが4
より小さいことが必要十分条件である.
である多項式が常に作れるためには,その区間の長さが4
より小さいことが必要十分条件である.
 したがって,
したがって, 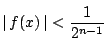 と仮定する. いま
と仮定する. いま
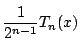 が
が
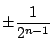 の値
をとる1から
の値
をとる1から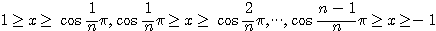
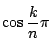 で一致したときを考える.
で一致したときを考える.
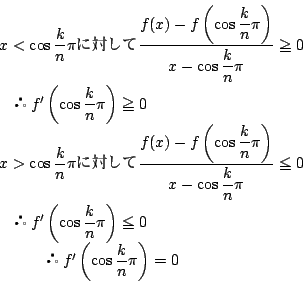
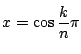 は方程式
は方程式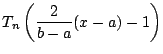 の最高次の項の係数は
の最高次の項の係数は
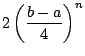 であった. よって,
であった. よって,
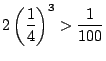 なので
不可能であるが,
なので
不可能であるが, 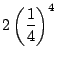 と
と
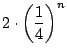 である. すると,
である. すると,