耕一 内分の方はよく知っていますが,外分は知りません.
南海 証明はベクトルを用いてはどうだろうか. 類似問題が09年の阪大にある.その解答を参考にして 証明してほしい.
耕一 はい.
証明
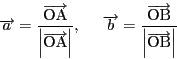
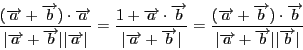
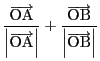 は
は
同様に二つの外角の一方を二等分する方向として
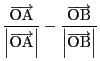 を用いることができる.
を用いることができる.
これら二等分の方向が直線![]() と交わる点を
と交わる点を
![]() とすると,
とすると,
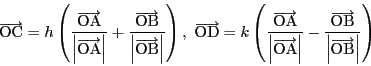
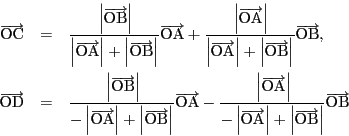
南海
線分![]() を
を
![]() が内分,外分しているとき,
一直線上の4点
が内分,外分しているとき,
一直線上の4点
![]() は
調和点列であるという.
「反転と円環問題」にもこの比は出てきていた.
は
調和点列であるという.
「反転と円環問題」にもこの比は出てきていた.
証明 中心に関する点
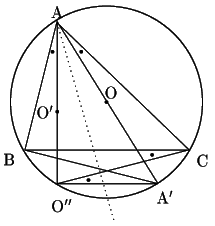
![]() の二等分線に関して直線
の二等分線に関して直線
![]() が対称の位置にあり,点
が対称の位置にあり,点
![]() も対称の位置にあるので,
も対称の位置にあるので,
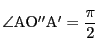 なので,
なので,
南海 もう一つ,内接円と傍接円の接点に関する補題が必要だ.
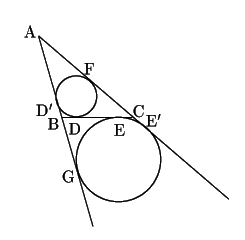 証明
図のように,内接円の他の辺との接点を
証明
図のように,内接円の他の辺との接点を
円の対称性から
![]() なので,
なので,
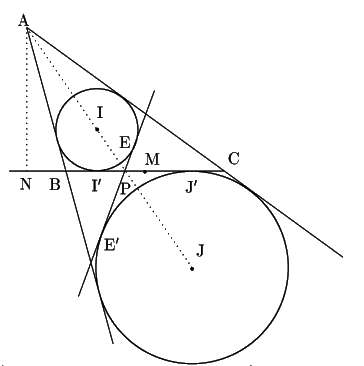 定理1の点の記号はそのまま用いる.
とくに
定理1の点の記号はそのまま用いる.
とくに
まず関係式
を示す.
![]() である.
である.
![]() の二等分線に関する
補題3より
の二等分線に関する
補題3より![]() は
は![]() と対称で,
と対称で,
![]() と
と![]() も同じ二等分線に関して対称である.したがって
も同じ二等分線に関して対称である.したがって
つぎに補題2から,点![]() と点
と点![]() は
は
![]() を
を
![]() に内分,外分する.よって
に内分,外分する.よって
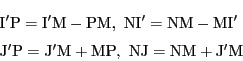
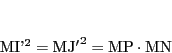
いま点![]() を反転の中心とし,
を反転の中心とし,![]() を反転の半径とする反転をとる.
方べきの定理よりこの反転で内接円と傍接円はそれ自身に移る.
また九点円は反転の中心
を反転の半径とする反転をとる.
方べきの定理よりこの反転で内接円と傍接円はそれ自身に移る.
また九点円は反転の中心![]() を通るので,ある直線
を通るので,ある直線![]() に反転される.
に反転される.
![]() における九点円の接線は九点円と
における九点円の接線は九点円と![]() の他に共有点はない.
したがって
の他に共有点はない.
したがって![]() は
は![]() における九点円の接線と共有点がない.
つまり,
における九点円の接線と共有点がない.
つまり,![]() は
は![]() における九点円の接線と平行である.
直線
における九点円の接線と平行である.
直線![]() は
は![]() における九点円の接線と平行であったので,
における九点円の接線と平行であったので,
![]() と直線
と直線![]() は平行である.
は平行である.
ところが関係式(5)は点![]() と点
と点![]() はこの反転に関して
互いに移ることを示している.九点円は点
はこの反転に関して
互いに移ることを示している.九点円は点![]() を通るので
を通るので![]() は点
は点![]() を通る.
この結果
を通る.
この結果![]() は直線
は直線![]() に一致する.
に一致する.
直線![]() は内接円,傍接円に接しているので,
反転で戻した九点円は内接円,傍接円と接している.
その接点は点
は内接円,傍接円に接しているので,
反転で戻した九点円は内接円,傍接円と接している.
その接点は点
![]() とこの反転で対応する点である.
□
とこの反転で対応する点である.
□
南海 ということなのだ.
耕一 接点も与えられるのですね. この接点の決め方と,幾何の証明での接点の決め方と, 同じ点を定めるのですね. 不思議な気がします.
南海 それは今後の課題としよう. さらにこの接点をさらに別の面からも特徴づけることができる. そこに進もう.