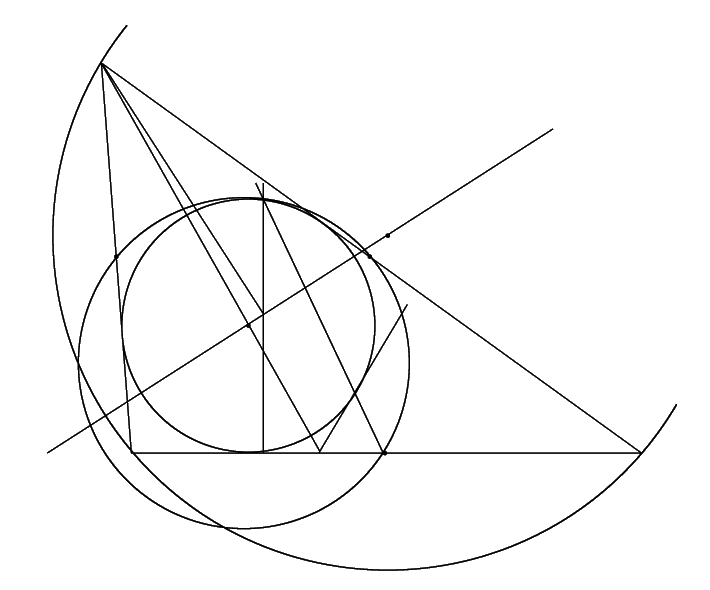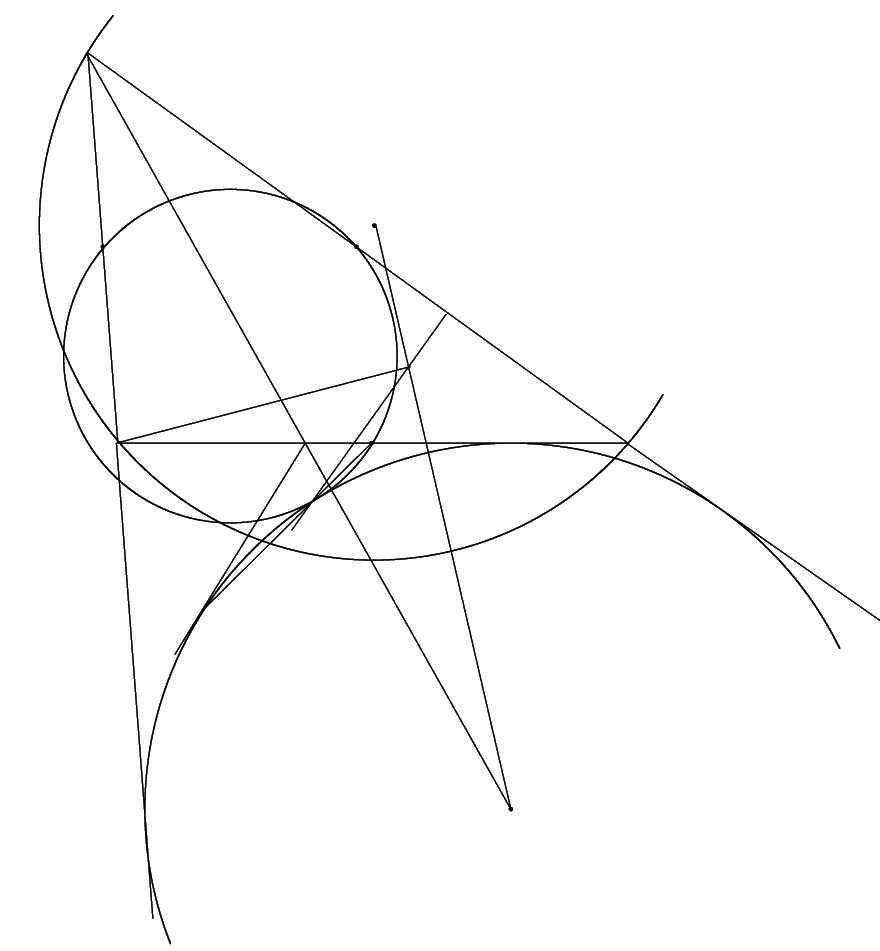この証明もいくつかある.
証明
 直線
直線![]() と
と
![]() の外接円の交点を
の外接円の交点を![]() とする.
とする.
![]() を通り
を通り![]() に平行な直線と直線
に平行な直線と直線![]() ,直線
,直線![]() との交点をそれぞれ
との交点をそれぞれ
![]() とする.
また
とする.
また![]() から直線
から直線![]() への垂線の足を
への垂線の足を![]() とする.
とする.
直線
![]() と直線
と直線![]() が直交することを示す.
そのためには
が直交することを示す.
そのためには
線分![]() を点
を点![]() が
が
![]() まで平行移動するとき
点
まで平行移動するとき
点![]() が異動する点を
が異動する点を![]() とする.
この方向と大きさの平行移動で点
とする.
この方向と大きさの平行移動で点![]() は
は
![]() に,
点
に,
点![]() は
は
![]() に移る.
に移る.
よって,点
![]() から直線
から直線![]() への垂線,
点
への垂線,
点
![]() から直線
から直線![]() への垂線,
点
への垂線,
点
![]() から直線
から直線![]() への垂線は1点
への垂線は1点![]() で交わる.
□
で交わる.
□
第二の証明
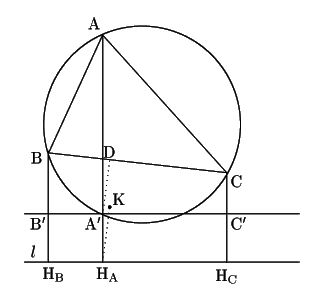
![]() の辺
の辺![]() と
と![]() の中点を
の中点を
![]() とする.
点
とする.
点![]() を中心とし2点
を中心とし2点
![]() ,
,
![]() を通る円がある.
また
点
を通る円がある.
また
点![]() を中心とし2点
を中心とし2点
![]() ,
,
![]() を通る円がある.
を通る円がある.
この2円の共通直線,つまり根軸は直線
![]() と直交する.
ところが
と直交する.
ところが
![]() なので
この根軸が
なので
この根軸が
![]() から辺
から辺![]() への垂線に他ならない.
への垂線に他ならない.
3円の3本の根軸は1点で交わるので,
点
![]() から直線
から直線![]() への垂線,
点
への垂線,
点
![]() から直線
から直線![]() への垂線は1点
への垂線は1点![]() で交わる.
□
で交わる.
□
耕一 各辺の中点を中心とし,角垂線の足を通る円の3本の根軸が1点で交わるというのは, 『数学対話』の「反転と円環問題」で読んだことがあります.
南海
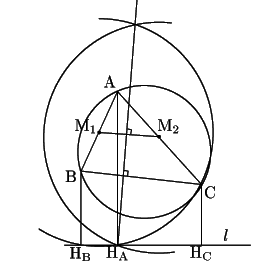
この準備を済ますと,九点円と内接円の接点が
直線![]() の直極点であることを示すことができる.
の直極点であることを示すことができる.
ある傍接円の傍心を![]() とする.
とする.
![]() の九点円とその傍接円は直線
の九点円とその傍接円は直線![]() の直極点で接する.
の直極点で接する.
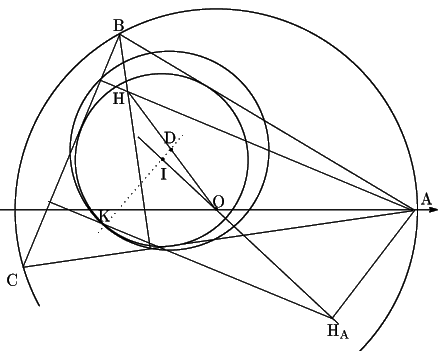
証明
正三角形ではないので,内心は外心と異なり,九点円と内接円も異なる.
定理1によって九点円と内接円は接する.
したがってその接点はそれぞれの中心を結ぶ直線![]() と九点円の交点である.
この交点を
と九点円の交点である.
この交点を![]() とする.
とする.
![]() が直線
が直線![]() の直極点であることを示す.
の直極点であることを示す.
そのために,
頂点![]() から直線
から直線![]() に下ろした垂線の足を
に下ろした垂線の足を
![]() とするとき,
とするとき,
その証明をつぎの三段階でおこなう.
(1)
![]() の外心を原点にとり定理1と同様に角を決める.
定理1の証明から
の外心を原点にとり定理1と同様に角を決める.
定理1の証明から
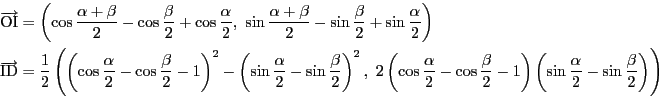
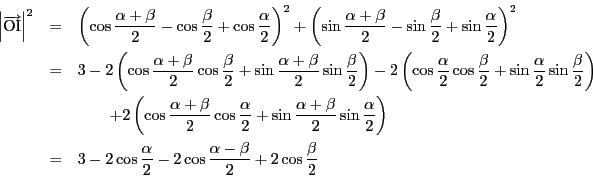
一方,等式(1)をさらに計算すると,
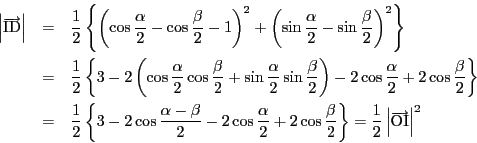
(2)
点![]() は点
は点![]() の直線
の直線![]() への正射影である.
への正射影である.
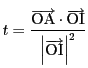 となる.よって
となる.よって
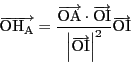
また点![]() は直線
は直線![]() 上に
上に
![]() の順にあり,
の順にあり,
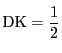 となるものなので,
となるものなので,
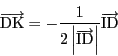
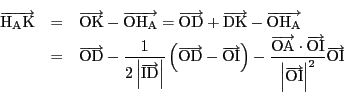
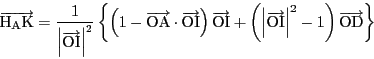
(3)
![]() を示す.
を示す.
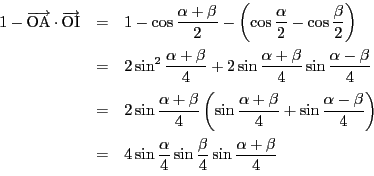
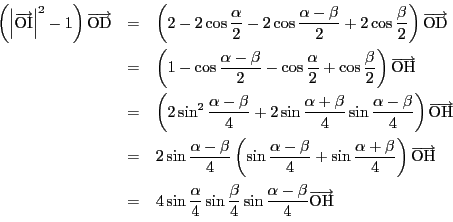
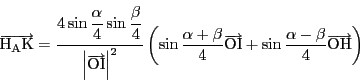
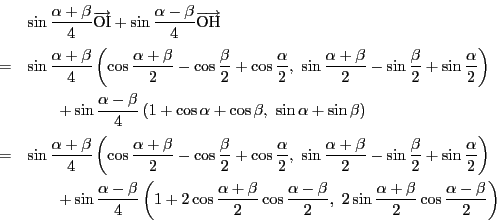
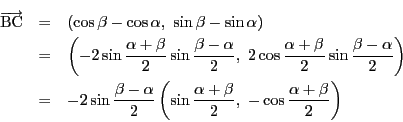
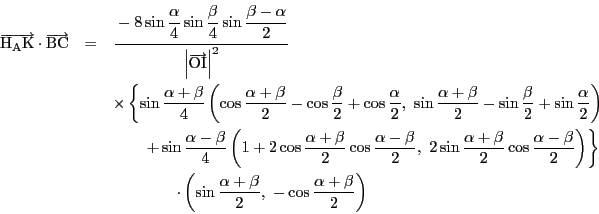
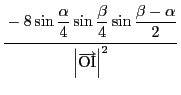 を除く部分を成分計算する.
を除く部分を成分計算する.
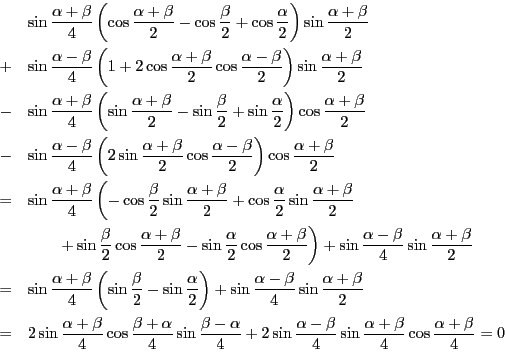
傍接円の場合の証明も同様である.この記述は略する. 以上から定理は証明された. □
耕一 計算量は多いですが,しかしうまく組みあわせるときれいな結果になるのですね.
南海 傍接円の場合の計算は略した.代わりに図を描いておこう.
いずれにせよ九点円と内接円または傍接円は接する.その接点は 外心と内心または傍心を結ぶ直線に関する直極点である. 同時にまたその接点は,辺の中点を中心とし内接円または傍接円の接点までの距離を半径とする反転で, その接点の頂角の二等分線に関する対称点が移る点でもある. あえて点に記号をつけず図そのものを示すのでよく味わってほしい.
耕一 見れば見るほど不思議です.