 解2
地表からテレビ塔の先端が重なって見えたので,3本とも長さが違う.
3本の長さを
解2
地表からテレビ塔の先端が重なって見えたので,3本とも長さが違う.
3本の長さを  と,
辺
と,
辺 ,
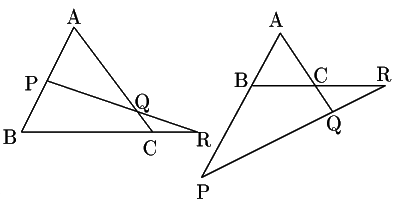
, ,
,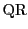 の延長線上の点
の延長線上の点
南海 今なら「ひとりの人」というところだが,「ひとりの男」と言うところにも問題の古さが現れている. これについては三通りの解法を『別解研究』の「空間図形のとらえ方」に「共線を示す[66年京大]」 として紹介した.「共線」とは点が直線を共にするということで,「3点が共線である」とは3点が同じ直線上にあるという意味である.また「共点」とは3本以上の直線が点を共有する,つまりその点で交わるという意味である.
太郎 私は,「3点が一直線上にある」,つまり3点が共線であることを示す証明問題なので, ベクトルを用いて解きました. そのうえで『別解研究』の別解を授業でも聞きました. そこでの解2と解3は大変明快です. もういちどここに書きます.
 解2
地表からテレビ塔の先端が重なって見えたので,3本とも長さが違う.
3本の長さを
解2
地表からテレビ塔の先端が重なって見えたので,3本とも長さが違う.
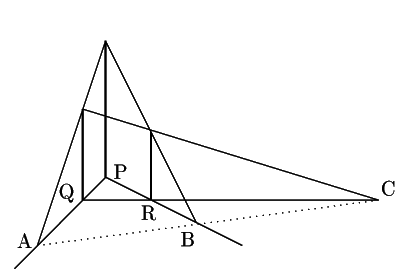
3本の長さを ![]() とし,テレビ塔と地表の交点をP,Q,R とする.
とし,テレビ塔と地表の交点をP,Q,R とする.
 と,
辺
と,
辺 ,
, ,
,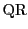 の延長線上の点
の延長線上の点
![]() に関してメネラウスの定理を用いる.
に関してメネラウスの定理を用いる.
太郎 これは簡明ですが平面ベクトルを用いる解答と同様に平面内の問題として考えています. しかし次の問題は空間図形を用います.
解3
テレビ塔の先端の3点が定める平面を ![]() とする.
3点A,B,C は
とする.
3点A,B,C は![]() 上にある.
一方,3点A,B,C は地表という平面上にもある.
ゆえに3点 A,B,C は
上にある.
一方,3点A,B,C は地表という平面上にもある.
ゆえに3点 A,B,C は ![]() と地表の交わりの直線上にある.□
と地表の交わりの直線上にある.□
南海
この問題は私が大学を受験したときの問題だ.
私は解2とは異なり,メネラウスの定理を
![]() と直線 QR に関して用いて解いた.
直線が三角形の外部にあるときのメネラウスの定理をよく知らなかったのだ.
直線
と直線 QR に関して用いて解いた.
直線が三角形の外部にあるときのメネラウスの定理をよく知らなかったのだ.
直線![]() と直線 QR の交点を
と直線 QR の交点を![]() として,
条件から
として,
条件から
![]() となることを示して解いたような気がする.
少し面倒だったがとにかく解けた.
となることを示して解いたような気がする.
少し面倒だったがとにかく解けた.
ところが,高校から一緒に受験した友だちと試験が終わってから話していると, 彼は「三行で済んだ」というのだ.それが解3だ. その解を聞いて驚いた.大変印象が深くてそれで今も覚えている. その人のことを『青空学園だより』に書いた.読んでほしい.
太郎 解2と解3はいずれも簡明です. 解2はほとんどメネラウスの定理と同じ内容です. とすると,この二つをつないで, メネラウスの定理を空間図形から証明することはできないのかと考えました.
南海 それはいい着眼だ.どこまでできたのか. まずメネラウスの定理を書き,証明の出来たところまでやってみてほしい.
太郎 普通は,メネラウスの定理とメネラウスの定理の逆とに分けます. それを一つにまとめると次のようになります. 京大の問題とは点の名称の系列が逆になります.
 定理 1
定理 1
![]() の
辺
の
辺![]() と
と![]() の上に点
の上に点
![]() をとり辺
をとり辺![]() の延長線上に点
の延長線上に点![]() をとるか,または
辺
をとるか,または
辺![]() ,
,![]() と辺
と辺![]() の延長線上に
それぞれ点
の延長線上に
それぞれ点
![]() をとる.
いずれの場合も,3点
をとる.
いずれの場合も,3点
![]() に関する次の二つの条件は同値である.
に関する次の二つの条件は同値である.
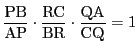 が成り立つ.
が成り立つ.
南海
これはよいまとめ方だ.
多くの参考書ではメネラウスの定理とその逆定理という二つの部分に分けている.
しかし,メネラウスの定理は
3点
![]() に関する二つの条件が同値
であることを言うものなのだ.
に関する二つの条件が同値
であることを言うものなのだ.
太郎
京大の問題を参考に,
3点
![]() が
が
![]() の外部にある場合が示せました.
の外部にある場合が示せました.
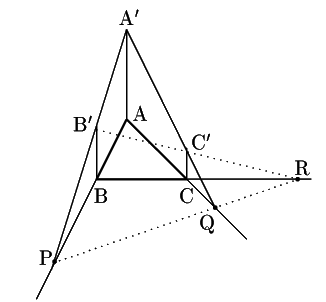 証明1
点
証明1
点![]() を
を![]() と
と
![]() が直交するように適当にとる.
同様に点
が直交するように適当にとる.
同様に点
![]() から
から
![]() に直交する直線を引いておく.
それらの直線と,
直線
に直交する直線を引いておく.
それらの直線と,
直線![]() ,
, ![]() との交点をそれぞれ
との交点をそれぞれ
![]() とおく.
このとき
とおく.
このとき
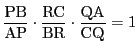 が成り立つことと,
3点
が成り立つことと,
3点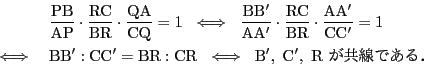
南海 メネラウスの定理を二つの構成部分に分解し, それぞれで同値性を示すというのは大変いい方針だ.
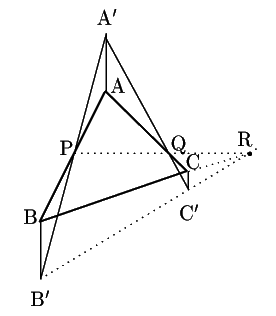
太郎
ところが2点
![]() が
が
![]() の辺上にある場合がうまく示せません.
の辺上にある場合がうまく示せません.
南海 それは簡単だ.図のように逆の方向にとればよい.
 太郎
そうか.点
太郎
そうか.点![]() を通り
を通り
![]() と直交する直線と,直線
と直交する直線と,直線![]() との交点を
との交点を![]() とすれば,まったく同様なのだ.証明も先の証明そのままです.ということは,これでメネラウスの定理を空間図形で証明することができました.
とすれば,まったく同様なのだ.証明も先の証明そのままです.ということは,これでメネラウスの定理を空間図形で証明することができました.
京大の問題を参考にしたので,
点![]() を
を![]() と
と
![]() が直交するように適当にとりました.しかしここは比率と4点
が直交するように適当にとりました.しかしここは比率と4点
![]() が同一平面上にあることだけを用いているので,
が同一平面上にあることだけを用いているので,![]() ,
,![]() ,
,![]() が平行であればよいです.
が平行であればよいです.
命題 1
平行な三直線
![]() ,
,
![]() ,
,
![]() がある.
がある.
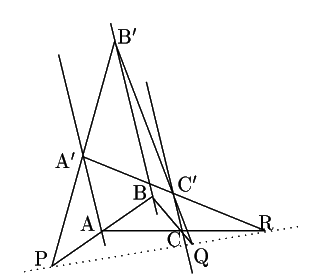 直線
直線![]() と
と![]() ,
直線
,
直線![]() と
と![]() ,
直線
,
直線![]() と
と![]() がそれぞれ
がそれぞれ
![]() で交わるなら,
で交わるなら,
![]() は共線である.
は共線である.
太郎 図を描いてみます. これを平面図形で証明するのはメネラウスの定理です.
しかしこの図を空間におかれた図と見れば,
3点
![]() は,
平面
は,
平面![]() と
平面
と
平面
![]() の交わる直線上にあるのは明らかです.
の交わる直線上にあるのは明らかです.
南海 今「明らか」といったことが射影の方法だ. 平面図形を空間におかれた図形の射影と見るのだ.
空間に図形,つまり空間における点の集合![]() があるとする.
空間に一点
があるとする.
空間に一点![]() と平面
と平面![]() をとる.点
をとる.点![]() と
と![]() の各点を結ぶ直線と
の各点を結ぶ直線と![]() の交点を
の交点を![]() 上にとることにより,平面図形
上にとることにより,平面図形![]() が得られる.
が得られる.
逆に平面図形![]() に対して,空間に点
に対して,空間に点![]() をとり,点
をとり,点![]() を
を![]() の各点を結ぶ直線上の
の各点を結ぶ直線上の![]() と異なる点をとる.空間図形
と異なる点をとる.空間図形![]() が得られる.
が得られる.![]() が点と直線でできた図形のときは,まず指定された点に対して
が点と直線でできた図形のときは,まず指定された点に対して![]() での点を決める.直線は直線上の2点に対応する点をとり,その2点を結ぶことで
での点を決める.直線は直線上の2点に対応する点をとり,その2点を結ぶことで![]() での位置を定める.
での位置を定める.
図形![]() は図形
は図形![]() の平面
の平面![]() への射影であるという.
このような対応を射影変換という.
への射影であるという.
このような対応を射影変換という.
この変換で,
![]() において交わる2直線は,
において交わる2直線は,![]() においても交わる2直線になる.
においても交わる2直線になる.
![]() において2点を通る直線は,
において2点を通る直線は,![]() においても対応する2点を通る直線になる.
においても対応する2点を通る直線になる.
従って,![]() において2直線が交わること,2点が定める直線上に第3の点が乗っていること等,
において2直線が交わること,2点が定める直線上に第3の点が乗っていること等,
![]() における点と直線の結合関係は,
における点と直線の結合関係は,![]() で同じ結合関係を満たすこと同値になる.
で同じ結合関係を満たすこと同値になる.
太郎
私は先ほど「空間におかれた図と見れば」といいましたが,
見ている目の位置が点![]() なのですね.
この方法では平行な直線は必ずしも平行にはなりません.また長さも変化します.線分の比も変わります.
このような性質はこの射影による対応では保たれないのですね.
なのですね.
この方法では平行な直線は必ずしも平行にはなりません.また長さも変化します.線分の比も変わります.
このような性質はこの射影による対応では保たれないのですね.
南海
今いったことで,長さが保たれないというのはその通りなのだ.
平行という条件は一点で交わるという条件と同じだ.
それはなぜか.このような問題を考えるときに,平面は射影平面で考える.
射影平面は「パスカルの定理」「パップスの定理」で定義した.
普通の![]() 平面にさらに無限直線を付け加える.
無限直線上の点を無限遠点という.平行な二直線は無限遠点で交わるとするのだ.
こうすることで平行と交わるは空間におかれた2直線に関して同じ条件になる.
平面にさらに無限直線を付け加える.
無限直線上の点を無限遠点という.平行な二直線は無限遠点で交わるとするのだ.
こうすることで平行と交わるは空間におかれた2直線に関して同じ条件になる.
太郎 平行も交わるも,空間の直線としては同一平面上にあるというひとつの条件として表されます.
南海 射影変換によって変わらない図形の性質を研究するのが射影幾何学なのだ.
メネラウスの定理の証明で,(i)と(ii)の二つの同値性に分けた.(i)は長さが関係している部分.これは比例の関係から相似であることを導き,同一直線上にあることを示した. (ii)は射影変換で変わらない部分である.
太郎 自分ではそのようにわかって二つの構成部分に分けたのではありませんが,なるほど. それぞれ異なる原理で論証したのですね.