次: 双対原理 上: デザルグの定理 前: メネラウスの定理再考

デザルグの定理

入試問題の逆命題

太郎　　 もう一つ質問があります．それは京大1966年の問題の逆問題は何か． またそれは成り立つのか，ということです．

南海　　 ある問題が解けたときに，その逆について考えるのはすばらしい． 京大の問題は空間におかれた直線に関するものだ．

太郎　　 はい．空間図形の問題として考えました． しかし3点 $\mathrm{P},\ \mathrm{Q},\ \mathrm{R}$は共線である， という結論に対する仮定は何なのか．それが分かりませんでした．

先ほどの命題1で少し見えてきました． これは平面図形の問題ですが，ここから類推すると， 逆を考えるときの仮定にあたるのは， 三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$が平行という条件ではないか． 先の命題を次のように空間図形の命題にいいかえます．

命題 2   空間に三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$がある． さらに，直線$\mathrm{AB}$と$\mathrm{A'B'}$， 直線$\mathrm{BC}$と$\mathrm{B'C'}$， 直線$\mathrm{CA}$と$\mathrm{C'A'}$がそれぞれ $\mathrm{P},\ \mathrm{Q},\ \mathrm{R}$で交わるとする． これを前提にする．

三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$が平行であるなら， $\mathrm{P},\ \mathrm{Q},\ \mathrm{R}$は共線である．

これが先の命題1を空間図形にいいかえたものです．

南海　　 そうだろうか． 平行という条件を仮定と見ぬいたのは，その通りなのだが， 直線$\mathrm{AB}$と$\mathrm{A'B'}$， 直線$\mathrm{BC}$と$\mathrm{B'C'}$， 直線$\mathrm{CA}$と$\mathrm{C'A'}$がそれぞれ $\mathrm{P},\ \mathrm{Q},\ \mathrm{R}$で交わるとする，を前提にしてよいか．

もしこの三つの直線の組がそれぞれ交わるのなら， $\mathrm{ABC}$平面と $\mathrm{A'B'C'}$平面の交わる直線上に $\mathrm{P},\ \mathrm{Q},\ \mathrm{R}$があるので共線は明らかだ．

太郎　　 確かに．すると先の命題の本質的な部分は次のようにしなければなりません．

命題 3   空間に三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$がある．

三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$が平行で， 直線$\mathrm{AB}$と$\mathrm{A'B'}$， 直線$\mathrm{BC}$と$\mathrm{B'C'}$が交わるなら， 直線$\mathrm{CA}$と$\mathrm{C'A'}$も交わる．

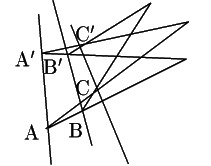
この逆は成り立つのでしょうか． つまり次の命題は成立するのでしょうか．

命題 4   空間に三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$がある．

直線$\mathrm{AB}$と$\mathrm{A'B'}$， 直線$\mathrm{BC}$と$\mathrm{B'C'}$, 直線$\mathrm{CA}$と$\mathrm{C'A'}$がそれぞれ交わるなら， 三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$は平行である．

南海　　 成り立つかどうかは，論証を進めて起こりうる場合を調べれば分かる．

空間の二直線は，一般的にはねじれの位置にある． ところが三組の直線がいずれもねじれの位置にはなく交わるというのだから， この命題の仮定は非常に強い条件であることが分かる．
太郎　　 直線$\mathrm{AB}$と$\mathrm{A'B'}$が交わるので$\mathrm{AA}'$，$\mathrm{BB}'$は同一平面上にある． 他も同様である．つまり$\mathrm{BB}'$，$\mathrm{CC}'$および$\mathrm{CC}'$，$\mathrm{AA}'$も同一平面上にある．

    直線 $\mathrm{AB}$，$\mathrm{A'B'}$， $\mathrm{BC}$，$\mathrm{B'C'}$， $\mathrm{CA}$，$\mathrm{C'A'}$がすべて同一平面上にあれば， $\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$も同一平面上にある．

直線 $\mathrm{AB}$，$\mathrm{A'B'}$， $\mathrm{BC}$，$\mathrm{B'C'}$， $\mathrm{CA}$，$\mathrm{C'A'}$がすべて同一平面上にあることはないとする．

$\mathrm{AA}'$，$\mathrm{BB}'$が交わるとき他の一組$\mathrm{BB}'$，$\mathrm{CC}'$も交わる． 必然的に $\mathrm{AA}'$，$\mathrm{CC}'$も交わり，三直線は1点で交わる．

逆に2本が平行なら他の1本もこれらに平行である．

よって3直線が同一平面にあるか，1点で交わるか，平行かのいずれかになる．

用いたことは二直線の組が同一平面上なるということなので， 結論とあわせて命題は次のようにいいかえなければなりませんでした．

命題 5        三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$がある．

直線$\mathrm{AB}$と$\mathrm{A'B'}$， 直線$\mathrm{BC}$と$\mathrm{B'C'}$, 直線$\mathrm{CA}$と$\mathrm{C'A'}$がそれぞれ同一平面上にあれば，

三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$のどの二本もそれぞれ同一平面上にある．

太郎　　 これが京大の問題の逆でした．

デザルグの定理

太郎　　 この形に定式化すればこの命題の逆が成り立つことも明らかです． つまり

命題 6        三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$がある．

このとき， 三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$のどの二本もそれぞれ同一平面上にあるならば， 直線$\mathrm{AB}$と$\mathrm{A'B'}$， 直線$\mathrm{BC}$と$\mathrm{B'C'}$, 直線$\mathrm{CA}$と$\mathrm{C'A'}$がそれぞれ同一平面上にある．

南海　　 命題5と命題6の同値性が， デザルグの定理といわれる定理の最も本質的なところだ． これを補題としてまとめておこう．

補題 1
空間におかれた異なる6点， $\mathrm{A},\ \mathrm{A}'$， $\mathrm{B},\ \mathrm{B}'$， $\mathrm{C},\ \mathrm{C}'$がある． 次の二つの条件は同値である．

(i)

直線$\mathrm{AB}$と$\mathrm{A'B'}$， 直線$\mathrm{BC}$と$\mathrm{B'C'}$, 直線$\mathrm{CA}$と$\mathrm{C'A'}$がそれぞれ同一平面上にある．

(ii)

三直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$のどの二本の組も それぞれ同一平面上にある．

南海　　 デザルグの定理は射影平面の定理として次の形でのべられる．

定理 2
射影平面におかれた $\bigtriangleup \mathrm{ABC}$と $\bigtriangleup \mathrm{A'B'C'}$がある． 次の二つの条件は同値である．

(i)

三直線$\mathrm{AA'}$，$\mathrm{BB'}$，$\mathrm{CC'}$が共点である(一点で交わる)．

(ii)

三つの直線の組$\mathrm{AB}$と$\mathrm{A'B'}$の交点， $\mathrm{BC}$と$\mathrm{B'C'}$の交点， $\mathrm{CA}$と$\mathrm{C'A'}$の交点の3点が共線である．

太郎　　 平行な場合が抜けると思いますが． いや．そうか，「一点で交わる」というとき，その交点が無限遠点の場合を含む， つまり三直線が平行であることがここに含まれているのですね． しかしそうすると$\mathrm{AB}$と$\mathrm{A'B'}$の交点などが無限遠点である場合もあるのですね．

そうか．それでも空間においたとき同一平面上にあるからいいのだ． 二直線が射影平面上で一点で交わることと， その二直線を空間においたとき，同一の平面上にあることが同じことなのだ．

また，(ii)は，三つの直線の組がそれぞれ交点をもつことが核心で， そのとき共線であることはすぐに分かるわけです．

定理2の証明      $\bigtriangleup \mathrm{ABC}$と $\bigtriangleup \mathrm{A'B'C'}$のおかれた平面に対して， この平面にない空間の点$\mathrm{O}$をとり，空間図形の射影が $\bigtriangleup \mathrm{ABC}$と $\bigtriangleup \mathrm{A'B'C'}$であるようにする．

対応する空間の点も同じ記号で表す． このとき，3直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$が一つの平面にのると， 3点 $\mathrm{A},\ \mathrm{B},\ \mathrm{C}$がすべて $\bigtriangleup \mathrm{ABC}$のある平面と，この平面の両方にあることになり，共線となって三角形の辺であることに反する． よって3直線$\mathrm{AA}'$，$\mathrm{BB}'$，$\mathrm{CC}'$が一つの平面上にあることはない．

補題1の(i)で2直線の三組が同一平面上にあることと， (ii)で3直線が同一平面上にあることが同値である． 定理2はこの場合を除いた場合なので， その同値性は補題1の同値性の直接の帰結である． □

南海　　 射影平面で考え平行であることを無限遠点で交わることとして，別に考えなかった． それは問題を単純化し明快にするのであるが，一方，あくまでこれまで通りの平面で考え， 平行な場合を場合に分けて見ていくことも面白い．
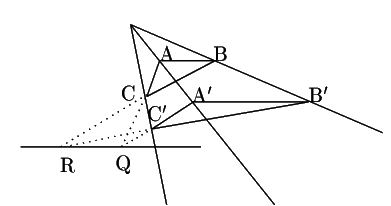
     例えば，$\mathrm{AB}$と$\mathrm{A'B'}$が平行な場合． $\mathrm{BC}$と$\mathrm{B'C'}$の交点$\mathrm{Q}$と， $\mathrm{CA}$と$\mathrm{C'A'}$の交点$\mathrm{R}$とこの無限遠点が共線ということは， $\mathrm{QR}$が$\mathrm{AB}$と平行であることを意味する． 実際これを描いてみると図のようになる．

この他いろいろな場合についても考えてみてほしい．

次: 双対原理 上: デザルグの定理 前: メネラウスの定理再考