射影平面である命題が成立すれば, その命題のなかの点と直線を入れ替え, 「点が直線の上にある」を「直線が点を通る」に入れ替えて作った命題も成立する.が成り立つ. これを双対原理といい, このようにして作られた命題をもとの命題の双対命題という. ではデザルグの定理の双対命題は何だろうか.
デザルグの定理で同値が示された二つの条件をもういちどよく見てみよう.
デザルグの定理2は射影平面上の6点
![]() ,
,
![]() ,
,
![]() からはじめた.
からはじめた.
これを6直線
![]() ,
,![]() ,
,![]() からはじめよう.
からはじめよう.
直線![]() は「点
は「点
![]() を通る直線」なので,
その双対は「
を通る直線」なので,
その双対は「![]() の交点」である.同様に考えデザルグの定理の二つの条件の双対条件をつくってほしい.
の交点」である.同様に考えデザルグの定理の二つの条件の双対条件をつくってほしい.
太郎 条件
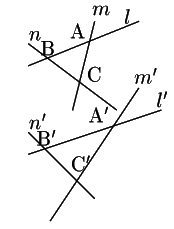 ところがここで次の図を見れば分かるように,
「
ところがここで次の図を見れば分かるように,
「したがって二つの条件の同値性を主張するデザルグの定理そのものである. このようにデザルグの定理は自己双対である.
ここを深く理解したいときは『幾何学の精神』にすすんでほしい.