 互いに外部にある,
中心を
互いに外部にある,
中心を
4本の共通接線が引ける. その6個の交点のうち相似の中心となるものが2個ある. 線分
 互いに外部にある,
中心を
互いに外部にある,
中心を
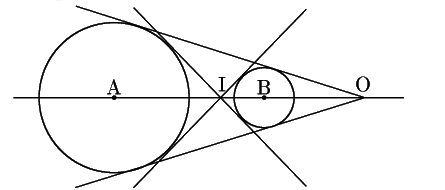
![]() とする二つの円がある.
とする二つの円がある.
4本の共通接線が引ける.
その6個の交点のうち相似の中心となるものが2個ある.
線分![]() の外分点となるものを外相似点,
内分点となるものを内相似点という.
これらが線分
の外分点となるものを外相似点,
内分点となるものを内相似点という.
これらが線分![]() を半径の比に外分する点と内分する点であることはただちにわかる.
を半径の比に外分する点と内分する点であることはただちにわかる.
この用語を用いるとモンジュの定理は次のようになる.
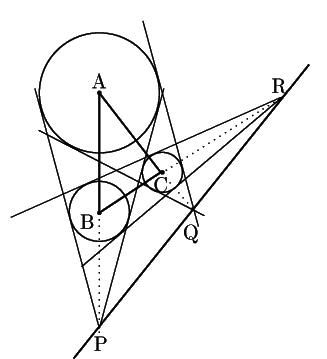 互いに外部にある3円がある.2円の外相似点が3個できるがそれらは共線である.
互いに外部にある3円がある.2円の外相似点が3個できるがそれらは共線である.
南海
3円の中心を
![]() とし,
とし,
![]() と三つの外相似点に関して
メネラウスの定理を用いることにより,これを示してほしい.
と三つの外相似点に関して
メネラウスの定理を用いることにより,これを示してほしい.
太郎
三つの外相似点を
![]() とし,
3円の半径を
とし,
3円の半径を
![]() とする.
このとき
とする.
このとき
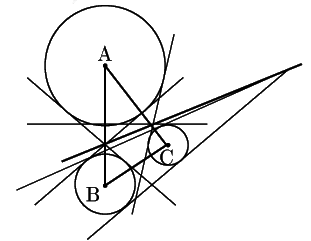 従って3点
従って3点
太郎 すると比率は同じことなので,二つの内相似点と一つの外相似点も共線ではありませんか.
南海 その通り.
別解 さて今回の平面図形を空間図形で示すという観点から, 三つの外相似点共線であることの別解を示そう. 図は描きにくいのだが,これを自分の頭の中で描いてほしい.
3点
![]() を中心とし,
半径が
を中心とし,
半径が
![]() の三つの球を考える.これらは中心の乗っている平面
の三つの球を考える.これらは中心の乗っている平面![]() に関して対称である.3球に接する平面が2枚できる.対称性からその交線
に関して対称である.3球に接する平面が2枚できる.対称性からその交線![]() は
は![]() 上にある.
上にある.
一方点![]() は
は![]() と
と![]() を中心とする2球の相似の中心なので,2球の共通接平面は点
を中心とする2球の相似の中心なので,2球の共通接平面は点![]() を通る.よって点
を通る.よって点![]() は
は![]() 上にある.
上にある.
![]() も
も![]() 上にある.
つまりこの3点は直線
上にある.
つまりこの3点は直線![]() 上にある.
上にある.
太郎 確かに.
南海 『数学対話』では「パスカルの定理」「パップスの定理」とそして今回の「デザルグの定理」と,射影幾何に関係する話題が3題になった.それぞれ具体的な問題から入っているので,射影座標は「パスカルの定理」にでているが双対原理は「パップスの定理」で出てくる,という具合で体系的にはなっていない.
いずれこれらをまとめてもう少し体系的に整理したいと思ってきた.それが現在進行中の『パスカルの定理と幾何学の精神』だ.ぜひこちらにすすんでほしい.