- (i)
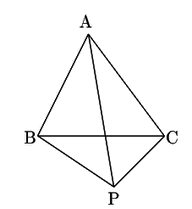
- 点Pは三角形ABCの内部(周は除く)にある
- (ii)
- 正の数
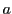 ,
,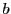 ,
,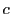 があって,
があって,
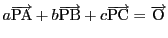 が成り立つ
が成り立つ
解答
点![]() が三角形
が三角形![]() の内部にあるとする.
線分
の内部にあるとする.
線分![]() の延長線が線分
の延長線が線分![]() (両端を除く)と交わる.
この点を
(両端を除く)と交わる.
この点を![]() とする.
とする.
逆に正の数![]() で
で
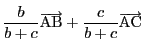 で定まる線分
で定まる線分 より点
より点
太郎
この問題の解をよく見ます.
正の数の組![]() に対して等式(2)で点
に対して等式(2)で点![]() が定まります.
が定まります.
![]() を正数として
を正数として
![]() も同じ点を定めます.
逆に
も同じ点を定めます.
逆に
![]() 内部の点
内部の点![]() に対して,
(1)で正の数の組
に対して,
(1)で正の数の組![]() の比が定まります.
の比が定まります.
そこで
![]() は固定したうえで,
は固定したうえで,
![]() が正という条件を外し
実数
が正という条件を外し
実数![]() を用いれば,数の組
を用いれば,数の組![]() で平面上の点を表すことができるのではないか.数の組
で平面上の点を表すことができるのではないか.数の組![]() に対して
に対して
逆に平面上の任意の点![]() に対して,
に対して,
![]() が一次独立であることより
が一次独立であることより
このように![]() である数の組
である数の組![]() と,
平面上の点が対応するのだから,
と,
平面上の点が対応するのだから,
![]() は座標ではないか,これが質問点です.
は座標ではないか,これが質問点です.
南海 まさにそうである.これは射影座標の一種と考えられる. 射影座標については既出のものでは『パスカルの定理』を, また今後書かれてゆく『幾何学の精神』を参考にしてほしい.
射影平面の射影座標![]() では
では![]() が無限遠直線となる.
ユークリッド平面は,射影平面で
が無限遠直線となる.
ユークリッド平面は,射影平面で![]() の部分であり,
の部分であり,
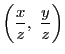 が
いわゆる
が
いわゆる![]() 座標平面の座標に対応する.
座標平面の座標に対応する.
等式(3)で点![]() を定める座標
を定める座標![]() では,
では,
![]() がいわば無限遠直線であり,
がいわば無限遠直線であり,
![]() の部分がユークリッド平面になる.
の部分がユークリッド平面になる.
ただここでは射影幾何の問題としてこれを考えるより, 19世紀に盛んに研究された三角形幾何の一つとして考え, この方向でパスカルの定理の別証明まで行ってみよう.
任意の基準点![]() をとって等式(3)を書き直すと
をとって等式(3)を書き直すと
一方
太郎
重心![]() は
は
内心![]() について.
について.
![]() の辺長を
の辺長を
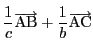 は
は
 となり,
となり,
南海 重心座標のもうひとつの意味を考えよう.
![]() を一つ固定する.
重心座標そのものは鋭角三角形を一つ固定すればよいのだが,
三頂点の位置ベクトルで,外心や垂心がどのように表されるかという観点から,
一般的に
を一つ固定する.
重心座標そのものは鋭角三角形を一つ固定すればよいのだが,
三頂点の位置ベクトルで,外心や垂心がどのように表されるかという観点から,
一般的に
![]() が鈍角三角形でもいいとする.
ただし垂心を考えるときは,直角三角形ではないとする.
が鈍角三角形でもいいとする.
ただし垂心を考えるときは,直角三角形ではないとする.
鈍角三角形の場合を含んで考えるために,その準備として,符号つき面積を定める.
![]() で図形としての三角形
で図形としての三角形![]() を表すが,
同時にその面積も表すことにする.
ただし,3点
を表すが,
同時にその面積も表すことにする.
ただし,3点
![]() が左回りに並んでいれば正の値にとり,
右回りに並んでいれば負の値にとるものとする.
すべて比が問題なので正負を逆にしても同じことである.
さらに3点
が左回りに並んでいれば正の値にとり,
右回りに並んでいれば負の値にとるものとする.
すべて比が問題なので正負を逆にしても同じことである.
さらに3点
![]() が同一直線上にあるときは0を表すものとする.
が同一直線上にあるときは0を表すものとする.
 このように約束すると,
このように約束すると,
![]() と点
と点![]() に対してつねに
に対してつねに
等式(4)は
 図のような位置に
図のような位置に![]() がある場合.
がある場合.
![]() は外分点である.符号も入れて
は外分点である.符号も入れて
始点を変えて考えることにより
太郎
つまり,
重心座標はまた点![]() を頂点とし,
を頂点とし,
![]() の各辺を
の各辺を![]() の対辺とする三角形の符号つき面積の値の比でもある.
絶対重心座標は
の対辺とする三角形の符号つき面積の値の比でもある.
絶対重心座標は
よって外心![]() の重心座標は
の重心座標は
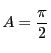 のときは
のときは
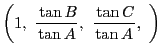 の極限で考え,
の極限で考え,南海 三角形には五心の他にも多くの点が定まる. それらの相互関係が,この重心座標や次に紹介する三線座標を用いて研究された. それは貴重なものであり,また実地に検証しながら証明してゆける分野で, 高校ではもっと取りあげてほしい.