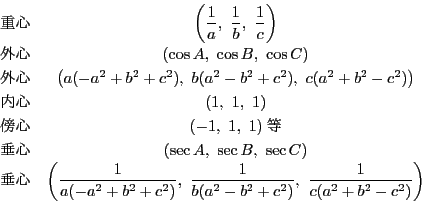次: 重心座標による図形の方程式 上: 重心座標 前: 重心座標と三角形の五心等

三線座標

南海　 重心座標と並んで三角形の幾何の研究などに用いられてきたのが 三線座標である．重心座標との関係でその定義と五心の表現には触れておこう．

三線座標の定義
平面上に $ \bigtriangleup \mathrm{ABC} $ をとる． 平面上の点 $ \mathrm{P} $ から 各辺 $ \mathrm{BC},\ \mathrm{CA},\ \mathrm{AB} $ ， またはその延長上に下ろした垂線の長さの比を $ x:y:z $ とする． ただし，内心と点 $ \mathrm{P} $ がその辺直線に関して同じ側にあるときは正，逆の側にあるときは負にとるものとする． 点 $ \mathrm{P} $ は比 $ x:y $ で上にあるべき直線が決まり， その結果，比 $ x:y:z $ で点 $ \mathrm{P} $ は一意に確定する． $ (x,\ y,\ z) $ を点 $ \mathrm{P} $ の三線座標という． 0でない実数 $ u $ に関して， $ (x,\ y,\ z) $ と $ (ux,\ uy,\ uz) $ は同じ点を定める． $ x,\ y,\ z $が長さそのもののときこれを\textbf{絶対三線座標}という．

ここで $ \bigtriangleup \mathrm{PQR} $ の面積を三点 $ \mathrm{P},\ \mathrm{Q},\ \mathrm{R} $ が反時計回りに配置されているとき正，一直線上にあるとき0，逆方向にあるとき負，と定める． $ (x,\ y,\ z) $ が点 $ \mathrm{P} $ の絶対三線座標であるとき， \[ \bigtriangleup \mathrm{PBC}=\dfrac{ax}{2},\ \bigtriangleup \mathrm{PCA}=\dfrac{by}{2},\ \bigtriangleup \mathrm{PAB}=\dfrac{cz}{2} \] となる．よって \[ ax+by+cz=2\bigtriangleup \mathrm{ABC} \] である．

太郎　 絶対三線座標では

$$\bigtriangleup \mathrm{PBC}=\dfrac{aX}{2},\ \bigtriangleup ... ...A}=\dfrac{bY}{2},\ \bigtriangleup \mathrm{PAB}=\dfrac{cZ}{2}$$

となる．よって

$$\dfrac{aX}{2}+\dfrac{bY}{2}+\dfrac{cZ}{2} =\bigtriangleup \mathrm{ABC}$$

である．

また点$\mathrm{P}$の重心座標を$(x,\ y,\ z)$， 三線座標を$(X,\ Y,\ Z)$とすると，

$$(x,\ y,\ z)=(aX,\ bY,\ cZ)$$

が成り立つ．

三角形の五心を三線座標で表すと次のようになる． 重心座標に現れた成分に対する主な計算では，

$$\dfrac{\sin2A}{a}=\dfrac{2\sin A\cos A}{2R \sin A}=\dfrac{\c... ...ac{\tan A}{2R \sin A}=\dfrac{1}{2R \cos A} =\dfrac{\sec A}{2R}$$

などより

$$\begin{array}{lc} 重心&\left(\dfrac{1}{a},\ \dfrac{1}{b},\... ...b(a^2-b^2+c^2)},\ \dfrac{1}{c(a^2+b^2-c^2)}\right) \end{array}$$

となる．