次： 根軸 上： 包絡線 前： 通過領域と境界の曲線

計算の実行

拓生　 計算をしてみます．2式を整理すると次のようになります．

$$(4t^3+4t)x+(-4t^2-4)y+(-t^4-t^2+1)=0$$

$t$ について微分すると次のようになります．

$$(6t^2+2)x+(-4t)y+(-2t^3-t)=0$$

この連立方程式を解くと，

$$x=\frac{2t^5+4t^3+4t}{4(t^2+1)^2}\,\,\,\,\,y= \frac{t^6+2t^4+4t^2+1}{4(t^2+1)^2}$$

となります．でもこのグラフは書けるのですか．

 

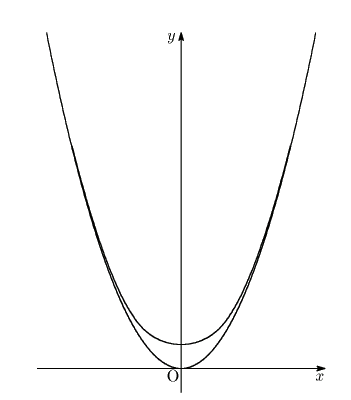
南海　それがパソコンを使えば書ける．細かく $t$ に値を代入していけばよい のだから．そのようにして得られたのが次のグラフだ．下にあるのが$y=x^2$ だ．

拓生　媒介変数表示されたものから $x$ と $y$ の関係式を求めることは できるのですか．

南海　 それもできるのだ． ここに『RISA/ASIR     日本で生まれた数式処理ソフト』（SEG出版）がある． これはたいへん強力なソフトで，しかも手軽に多項式の計算なんかに使える． これで， $t$ を消去してみよう．

すると，

$$\begin{eqnarray*} &&-1024x^6+(-2048y^2+4352y-752)x^4\\ && \quad \quad +(-1024... ... && \quad \quad \quad +1024y^5-1280y^4+1152y^3-544y^2+180y-25=0 \end{eqnarray*}$$

となるというのだ．

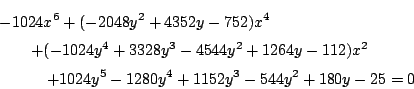
以上でかっぱさんの答えになっただろうか．

次の問題を，この方法で解いてみよう．

演習 2 ［97東大文系］　解答2

$ 0 \leqq t \leqq 1 $ をみたす実数 $ t $ に対して， $ xy $ 平面上の点A，Bを \[ \mathrm{A} \left(\dfrac{2(t^2+t+1)}{3(t+1)},\ -2 \right),\ \mathrm{B} \left(\dfrac{2}{3}t,\ -2t \right) \] と定める． $ t $ が $ 0 \leqq t \leqq 1 $ を動くとき，直線ABの通りうる範囲を求めよ．

演習 3 　解答3

$ x $ 軸上の点 $ \mathrm{A} $ と $ y $ 軸上の点 $ \mathrm{B} $ が， $ \mathrm{AB}=1 $ を満たして動くとき，線分 $ \mathrm{AB} $ の通りうる範囲を求めよ．