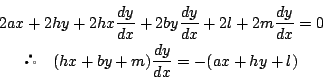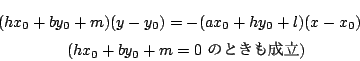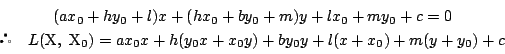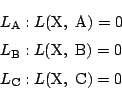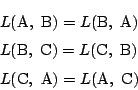解答 2
問題
2
直線ABの式は
\begin{eqnarray*}
y&=&
\dfrac{-2-(-2t)}{\dfrac{2(t^2+t+1)}{3(t+1)}-\dfrac{2t}{3}}\left(x-\dfrac{2t}{3}\right)-2t\\
&=&3(t^2-1)x-2t^3 \quad (0\leqq t \leqq 1)
\end{eqnarray*}
ここで
\[
a(t)=3(t^2-1),\ b(t)=-1,\ c(t)=-2t^3
\]
とおくと,直線ABは
\[
a(t)x+b(t)y+c(t)=0
\]
直線ABの包絡線を $ (x(t),\ y(t)) $ とおく. これは
\[
\left\{
\begin{array}{l}
a(t)x(t)+b(t)y(t)+c(t)=0\\
a'(t)x(t)+b'(t)y(t)+c'(t)=0
\end{array}
\right.
\]
をみたす.
$ a'(t)=6t,\ b'(t)=0,\ c'(t)=-6t^2 $ なので
\[
\left\{
\begin{array}{l}
3(t^2-1)x(t)-y(t)-2t^3=0\\
6tx(t)-6t^2=0
\end{array}
\right.
\]
$ t\ne 0 $ のとき $ x(t)=t,\ y(t)=t^3-3t $ .これが $ t\ne 0 $ 以外で成立するので,
$ t=0 $ でも成立する.
つまり包絡線は $ y=x^3-3x $ である.
したがって直線ABは $ y=x^3-3x $ の接線で, $ 0\leqq t \leqq 1 $ の範囲の接線の通過領域なので
求める領域は,次の図になる.
解答 3
問題
3
$ \mathrm{A}(a,\ 0),\ \mathrm{B}(0,\ b) $ とすると,条件は $ a^2+b^2=1 $ である.
そこで, $ a=\cos\theta $ , $ b=\sin\theta $ とおく.直線 $ \mathrm{AB} $ の方程式は
\[
x\sin\theta+y\cos\theta=\sin\theta\cos\theta=\dfrac{1}{2}\sin2\theta
\cdots④
\]
である.この両辺を $ \theta $ で微分する.
\[
x'\sin\theta+x\cos\theta+y'\cos\theta-y\sin\theta=\cos2\theta
\]
一般論から
\[
x'\sin\theta+y'\cos\theta=0
\]
なので,
\[
x\cos\theta-y\sin\theta=\cos2\theta
\cdots⑤
\]
$ ④, ⑤ $ を連立して解くことにより,
\begin{eqnarray*}
x&=&\cos2\theta\cos\theta+\dfrac{1}{2}\sin2\theta\sin\theta\\
&=&\dfrac{1}{2}\left(\cos3\theta+\cos\theta \right)
-\dfrac{1}{4}\left(\cos3\theta-\cos\theta \right)\\
&=&\dfrac{3}{4}\cos\theta+\dfrac{1}{4}\cos(-3\theta)=\cos^3\theta\\
y&=&-\cos2\theta\sin\theta+\dfrac{1}{2}\sin2\theta\cos\theta\\
&=&-\dfrac{1}{2}\left(\sin3\theta-\sin\theta \right)
+\dfrac{1}{4}\left(\sin3\theta+\sin\theta \right)\\
&=&\dfrac{3}{4}\sin\theta+\dfrac{1}{4}\sin(-3\theta)=\sin^3\theta
\end{eqnarray*}
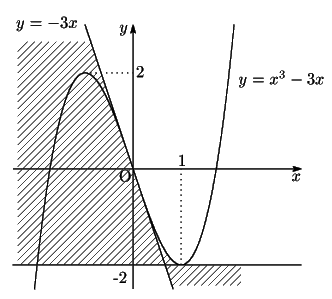
これは,半径1の円内を半径 $ \dfrac{1}{4} $ の円が動く,内サイクロイドである.
『数学対話』「光線の包絡線」参照.
したがって,線分 $ \mathrm{AB} $ の通過領域は,図の斜線部分である.
解答 3
問題3
-
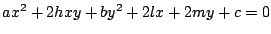 の両辺を
の両辺を 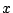 で微分すると
で微分すると
したがって, 点 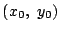 における接線の方程式は
における接線の方程式は
ここで,
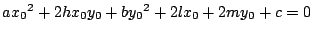 より
より
このとき
-
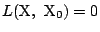 と
と
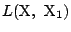 の交点をPとすると
,
の交点をPとすると
,
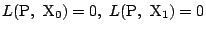 より,
より,
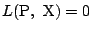 は直線
は直線
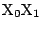 の方程式を表す.
すなわち
の方程式を表す.
すなわち
- 直線
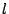 上の点Qより, 2本の接線
上の点Qより, 2本の接線
を引く. このとき, 直線
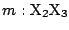 上に点Pがあることを示す.
上に点Pがあることを示す.
Qが
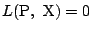 上にあるので
上にあるので
一方, 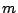 の方程式は(2)より,
の方程式は(2)より,
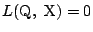 と書ける.
すると,
と書ける.
すると,
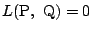 はPが直線
はPが直線
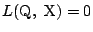 上にあることを示している.□
上にあることを示している.□
解答 4
問題
4
- 2直線
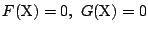 の交点の座標を
の交点の座標を
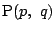 とおく. このとき
とおく. このとき
であるから,
よって,この直線は点Pを通る.また
であるから, この直線は 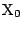 を通る.
を通る.
すなわち, 与えられた方程式はこの2点を通る一次式であるから,
この直線の方程式に他ならない.
-
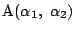 ,
,
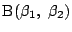 ,
,
 とすると,
とすると, 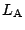 ,
, 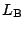 ,
, 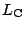 の
方程式は
の
方程式は
よって,
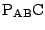 ,
,
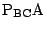 ,
,
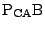 の方程式は
の方程式は
すると, 前問(1)の結果より,
だから, 1と2の辺々を加えて得られる式が 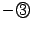 に他ならないことがわかる.
に他ならないことがわかる.
したがって,
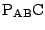 と
と
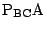 の交点を
の交点を 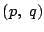 とおけば,
とおけば, 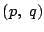 は1と2の両方の方程式を満足する
から,
は1と2の両方の方程式を満足する
から,
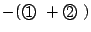 , すなわち3も満足する.
, すなわち3も満足する.
つまり, 交点は
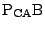 上にもあるので, これら三つの直線は1点Pで交わる.
上にもあるので, これら三つの直線は1点Pで交わる.
- ABと
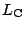 の交点をMとする. このとき, 前問(2)より, A, B
は
の交点をMとする. このとき, 前問(2)より, A, B
は
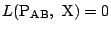 上にある.
上にある.
すると, 方程式
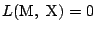 で表される直線は, Cと, M
からのもう一つの接点Dに対して, 直線CDを表す.
で表される直線は, Cと, M
からのもう一つの接点Dに対して, 直線CDを表す.
ところが, 前問(3)より,
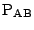 はCD上にある.
はCD上にある.
よって,
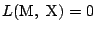 は直線
は直線
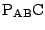 , すなわち,
上の1と一致する.
, すなわち,
上の1と一致する.
同様に, BCと 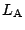 の交点Nに対して,
の交点Nに対して,
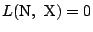 は
上の2と一致し, CAと
は
上の2と一致し, CAと 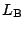 の交点Kに対し,
の交点Kに対し,
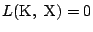 は
上の3と一致する. そして, これら三つの直線はすべてPを通るので,
は
上の3と一致する. そして, これら三つの直線はすべてPを通るので,
したがって, 三つの交点は一つの直線
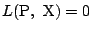 上にある.□
上にある.□


 次: 入試問題一覧
上: 幾何分野
前: 複素射影空間内での証明
Aozora Gakuen
次: 入試問題一覧
上: 幾何分野
前: 複素射影空間内での証明
Aozora Gakuen
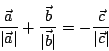
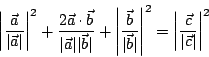
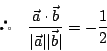
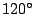
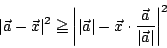
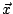 と
と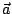 のなす角を
のなす角を 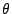 とすると
とすると
 はすべての内角が
はすべての内角が 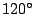 未満で
あるから,
未満で
あるから,
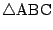 の内部の点
の内部の点 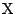 で
で
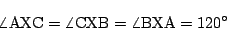
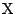 が題意をみたすことを示す.
が題意をみたすことを示す.
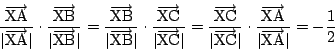
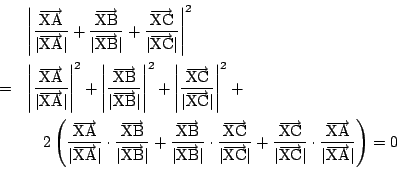
 をとる.(2)から
をとる.(2)から
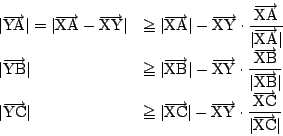
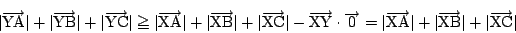
 が題意をみたすことが示された.
が題意をみたすことが示された.