![]() に対し
に対し ![]() の二変数の多項式を
の二変数の多項式を ![]() のように表す.
のように表す.
を実数係数の二次式とする.
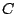 上の点
上の点
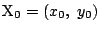 での
での 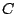 の接線の方程式のうち,
の接線の方程式のうち,
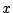 の係数が
の係数が 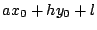 となるものを
となるものを
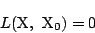
とする.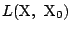 を求め
を求め
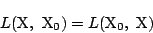
を示せ.- 曲線の外の点P
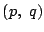 から曲線に2本の接線が引けるとする.このとき,
2接点を結ぶ直線
から曲線に2本の接線が引けるとする.このとき,
2接点を結ぶ直線 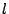 は,
は,
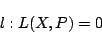
と書けることを示せ. 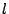 上の点Qからも曲線に2本の接線が引けるとする.このとき,
2接点を結ぶ直線
上の点Qからも曲線に2本の接線が引けるとする.このとき,
2接点を結ぶ直線 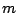 はPを通ることを示せ.
はPを通ることを示せ.
最初の問題はすでに計算を済ませているが,学校での演習用にここで再掲する.
![]() に対し
に対し ![]() の二変数の多項式を
の二変数の多項式を ![]() のように表す.
のように表す.
前問を前提に次の問いに答えよ.
3直線
![]() ,
,
![]() ,
,
![]() が互いに交わるならば,
これらは1点で交わることを示せ.
が互いに交わるならば,
これらは1点で交わることを示せ.

高校範囲で問題を設定した.そうすると,接線が平行で交点がない場合は,どのようになるのか,が問題になる.
これは,射影平面において考えればよい.その場合をふくめて統一的に証明される.確認してほしい.
また,
『
幾何学の精神
』のなかの
「
パスカルの定理
」
を参照してほしい.パスカルの定理のさまざまの証明を紹介している.