伍郎 いろんな観点というと, ベクトル,座標,図形の論証,などですか.
南海 これは実は前に考えた「パスカルの定理」からの帰結でもある. これも紹介しよう.
まず,普通にユークリッド平面,
つまり高校生が毎日見ている![]() 平面などで,考えていこう.
平面などで,考えていこう.
ベクトルでやるのと,座標でやるのは本質的には同じことだ.
ただ,ユークリッド平面で考える以上,
![]() が平行な場合は別に考えなければならない.
が平行な場合は別に考えなければならない.
![]() が平行な場合,座標ではどのようになるか.
が平行な場合,座標ではどのようになるか.
伍郎
図のように![]() 平面においてよい.
相似な拡大や縮小をしても一般性は失われないので,
平面においてよい.
相似な拡大や縮小をしても一般性は失われないので,
![]() の間の距離は1とする.
の間の距離は1とする.
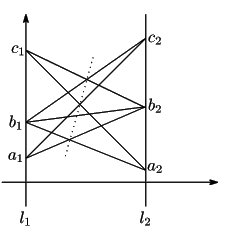
![]() 上に点
上に点
![]() の
座標を,
の
座標を,
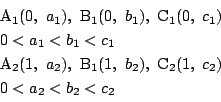
とする.
直線
![]() と直線
と直線
![]() の交点を
の交点を![]() ,
直線
,
直線
![]() と直線
と直線
![]() の交点を
の交点を![]() ,
直線
,
直線
![]() と直線
と直線
![]() の交点を
の交点を![]() とする.
とする.
このとき3点
![]() は一直線上にある.
は一直線上にある.
そこで,
![]() ,
,
![]() の交点
の交点![]() を
を![]() とおく.
とおく.
![]() ,
,
![]() が
ともに一直線上にあるので,
が
ともに一直線上にあるので,
![]() ,
,
![]() である.
平行条件を成分で書いて
である.
平行条件を成分で書いて
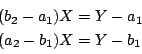
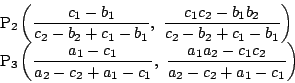
伍郎 これを計算するのですか.
南海 もうひとがんばり
伍郎 したがって
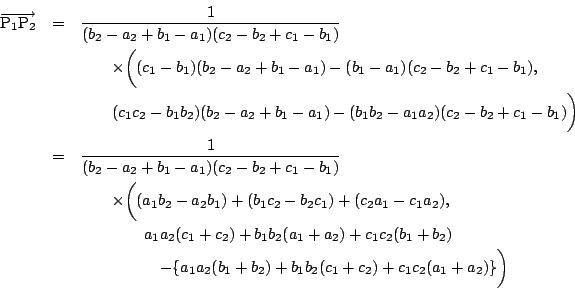
南海
![]() は,
は,
![]() において
において
伍郎 あっ,そうか.
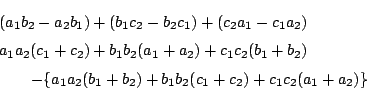
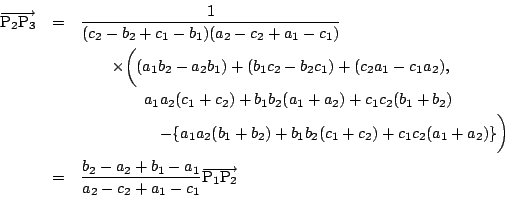
南海 というわけだ.
![]() が平行でない場合,これを参考にベクトルでやってみよう.
が平行でない場合,これを参考にベクトルでやってみよう.
![]() の交点を
の交点を![]() とし,
とし,![]() に対して,
に対して,
![]() 方向の長さ1のベクトルを
方向の長さ1のベクトルを
![]() とする.
また
とする.
また
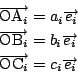
伍郎
ここからは私のはじめのやり方でと
先の座標の場合をあわせると,できそうです.
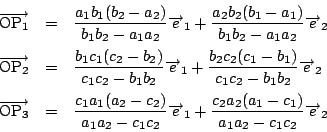
これから
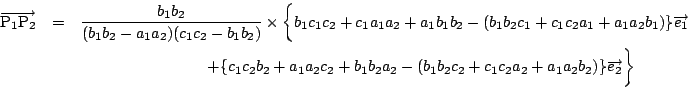
![]() はこの式において,
文字を
はこの式において,
文字を
![]() の順に置きかえたものである.
の順に置きかえたものである.
ところが
![]() ,
,
![]() ,
,
![]() ,
,
![]() は,いずれもこの置きかえで不変である.
は,いずれもこの置きかえで不変である.
よって
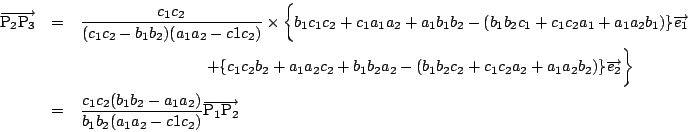
よって,3点
![]() は同一直線上にある.
は同一直線上にある.
南海 そう.それでベクトルによる証明が出来た.
伍郎
![]() と
と![]() が平行な場合と式はそんなに変わりません.
むしろベクトルを使った場合の方が簡単です.
が平行な場合と式はそんなに変わりません.
むしろベクトルを使った場合の方が簡単です.
南海
ベクトルで位置を表すのは,
斜交座標と考えれば,座標の複雑さでいえば,
直交座標の![]() 軸上と
軸上と![]() 軸上にそれぞれ3点が並んでいるようなものだから,
それほど複雑にはならない.
軸上にそれぞれ3点が並んでいるようなものだから,
それほど複雑にはならない.
伍郎 そうか.ベクトルのいいところですね.