南海
これは先に![]() と
と![]() が点
が点![]() で交わる場合を考えよう.
で交わる場合を考えよう.
直線
![]() と直線
と直線
![]() ,
直線
,
直線
![]() と直線
と直線
![]() が
いずれも平行ならそれほど難しくはない.
が
いずれも平行ならそれほど難しくはない.
これらのなかに平行でないものがあるとして,
直線
![]() と直線
と直線
![]() ,
が平行でないとする.
,
が平行でないとする.
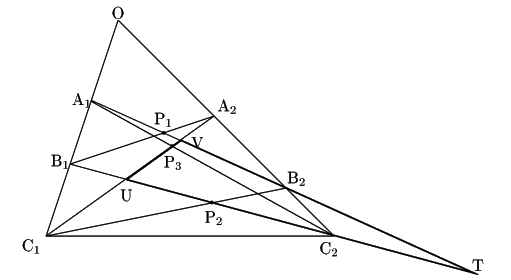 直線
直線
![]() と直線
と直線
![]() の交点を
の交点を![]() ,
,
![]() と
と
![]() の交点を
の交点を![]() ,
,
![]() と
と
![]() の交点を
の交点を![]() とする.
とする.
![]() とその辺の延長と交わる直線について
メネラウスの定理を用いる.
とその辺の延長と交わる直線について
メネラウスの定理を用いる.
直線
![]() に
関してメネラウスの定理を用いる.次の関係式を得る.
に
関してメネラウスの定理を用いる.次の関係式を得る.
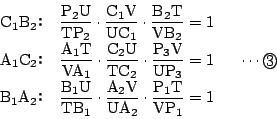
また
直線
![]() に
関してメネラウスの定理を用いる.次の関係式を得る.
に
関してメネラウスの定理を用いる.次の関係式を得る.

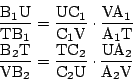
伍郎 わかりました.
![]() の3式をすべてかけあわせ,
の3式をすべてかけあわせ,![]() を代入することにより
を代入することにより
南海 ということだ.
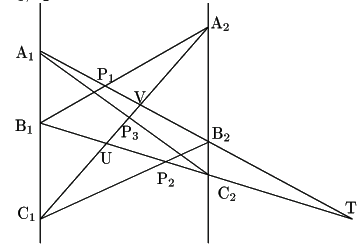 伍郎
伍郎
![]() が平行なとき,図を書いてみます.
が平行なとき,図を書いてみます.
同じようにやると,点の名前も同様につけられます.
![]() とその辺の延長と交わる直線について
メネラウスの定理を用いると,
とその辺の延長と交わる直線について
メネラウスの定理を用いると,
![]() と
と![]() が交わる場合の証明がすべてそのまま使えます..
が交わる場合の証明がすべてそのまま使えます..
南海
そうなのだ.![]() と
と![]() が交わる場合の証明で
「
が交わる場合の証明で
「
![]() に関してメネラウスの定理を用いる」
というところを,
「
に関してメネラウスの定理を用いる」
というところを,
「![]() と
と![]() に関してメネラウスの定理を用いる」とかえれば,
その他は同じなのだ.
に関してメネラウスの定理を用いる」とかえれば,
その他は同じなのだ.
![]() と
と![]() が交わることは何も使っていない.
が交わることは何も使っていない.