伍郎 射影平面で成り立つ図形の射影幾何学的な性質とはどのようなことですか.
南海 直線が2点を通るとか、2直線が交わるとか, 3点が一直線上にあるとか,3直線が1点で交わるとか, 点や直線から成り立つ平面上の図形の性質で, その図形をある点光源から他の平面に射影した影においても, 同じ性質が成立するような,図形の性質だ.
伍郎 平行光線ではなく点光源なのですね.
南海 そうなのだ.普通の平面図形というのはユークリッド平面, それに対して,無限遠点を加えた平面が射影平面だ.
点光源からの射影ということと,無限遠点との関係については, 参考文献などを読んでみてほしい.
射影平面では次のことが成り立つ.
距離のような量関係からは自由である. だから無限遠も,関係ない.
このような射影平面を座標で実現するには次のようにするのだった. これは,射影平面の座標による定義でもあり, また射影平面の公理を満たすモデルの提示でもある.
射影平面の座標を
![]() とする.
とする.
![]() のときはこの点は
のときはこの点は
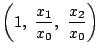 と同一視される.
これは2つの座標の空間,つまり平面と同じものである.
と同一視される.
これは2つの座標の空間,つまり平面と同じものである.
今までの平面(ユークリッド平面,![]() 平面)は,
射影平面のうち
平面)は,
射影平面のうち![]() の部分である.
の部分である.
伍郎
もとの3次元空間で,無限平面上の点![]() で交わる2直線を,
方向を適当にとって
で交わる2直線を,
方向を適当にとって
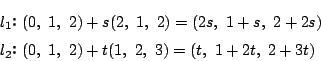
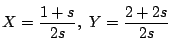 とおくと,
方程式は
とおくと,
方程式は
後の方で
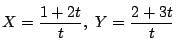 とおくと,
方程式は
とおくと,
方程式は![]() です.
です.
たしかに無限遠点で交わる2直線は, ユークリッド平面では平行2直線になります.
南海 それを直線方程式の方でも確認しよう.
![]() 平面での直線の方程式
平面での直線の方程式![]() を射影平面の方程式にするために,
を射影平面の方程式にするために,
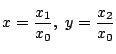 を代入して分母を払う.
を代入して分母を払う.
伍郎
平行2直線![]() と
と
![]() は
射影平面で方程式を表すと,
は
射影平面で方程式を表すと,
これは『パスカルの定理』にありました.
南海 ユークリッド平面の幾何学のどのような定理が射影幾何の定理に移るのかということはしっかりと考えなければならない. あるいは射影平面で考えることで, どのような一般化ができるのかもよく考えなければならない. 射影平面で考えるときは平行な場合を分ける必要がなくなる.
さて射影幾何では次のようなことができる.
2つの射影平面を用意する.
![]() と
と
![]() とする.
とする.
![]() の直線
の直線
![]() に対して
に対して
![]() の点
の点![]() を対応させる.
を対応させる.
![]() の点
の点![]() に対して
に対して
![]() の直線
の直線
![]() を対応させる.
を対応させる.
比が同じなら点も直線も同一なので,この対応はうまく定義される.
さて,![]() の
2直線
の
2直線
![]() ,
,
![]() が,
点
が,
点
![]() で交わるということは
で交わるということは
伍郎
対応するものは
![]() の2点
の2点![]() ,
,
![]() と,
直線
と,
直線
![]() です.
です.
だから,
![]() は
は
![]() の2点
の2点![]() ,
,
![]() が
直線
が
直線
![]() 上
にあるということを示しています.
上
にあるということを示しています.
ということは![]() の2点が同じ直線上にあれば,
の2点が同じ直線上にあれば,
![]() での対応物は,2直線が1点で交わる,
ということになります.
での対応物は,2直線が1点で交わる,
ということになります.
南海
だから,射影的なある性質が![]() で成り立てば,
点と直線を入れ替え,そのとき,
「1直線上にある2点」を「1点で交わる2直線」に入れ替え,
「2直線の交点」を「2点を通る直線」の入れ替えて作った
で成り立てば,
点と直線を入れ替え,そのとき,
「1直線上にある2点」を「1点で交わる2直線」に入れ替え,
「2直線の交点」を「2点を通る直線」の入れ替えて作った
![]() での命題も成り立つのだ.
証明もすべて対応する置きかえを作っていけばよい.
での命題も成り立つのだ.
証明もすべて対応する置きかえを作っていけばよい.
 そして,
そして,
![]() も
も
![]() もいずれも射影平面であることは変わらない.
だから,射影平面である定理が証明できれば,
点と直線を入れ替え,そのとき,
「1直線上にある2点」を「1点で交わる2直線」に入れ替え,
「2直線の交点」を「2点を通る直線」の入れ替えて作った
命題も成立する.
もいずれも射影平面であることは変わらない.
だから,射影平面である定理が証明できれば,
点と直線を入れ替え,そのとき,
「1直線上にある2点」を「1点で交わる2直線」に入れ替え,
「2直線の交点」を「2点を通る直線」の入れ替えて作った
命題も成立する.
これを双対原理といい,
このようにして作られた命題をもとの命題の双対命題という.
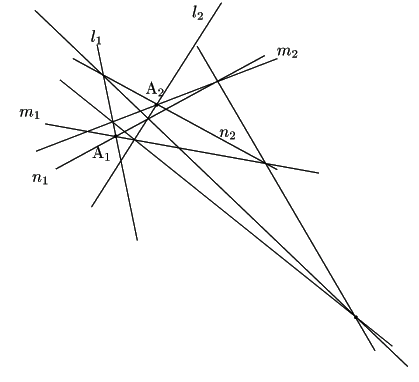
パップスの定理の双対命題は何か.
伍郎 次のようになります.
定理 3 (パップスの定理の双対命題)
2点![]() ,
, ![]() がある.
それぞれの点を通る直線
がある.
それぞれの点を通る直線
![]() と
と
![]() がある.
がある.
このとき,
![]() と
と![]() の交点と
の交点と![]() と
と![]() の交点を結ぶ直線
の交点を結ぶ直線![]() ,
,
![]() と
と![]() の交点と
の交点と![]() と
と![]() の交点を結ぶ直線
の交点を結ぶ直線![]() ,
,
![]() と
と![]() の交点と
の交点と![]() と
と![]() の交点を結ぶ直線
の交点を結ぶ直線![]() は1点で交わる.
は1点で交わる.
図をかいてみると確かに成り立っています.