次: 射影幾何的証明 上: パップスの定理 前: 射影平面と双対原理

射影変換

南海　 $xy$平面では，合同変換や相似変換，1次変換など， いろんな変換があった．

射影幾何学の基本的な要素と関係を保つような変換を射影変換という．

座標で表すと 点 $(x_0,\ x_1,\ x_2)$を

$$\begin{array}{l} X_0=a_{00}x_0+a_{01}x_1+a_{02}x_2\\ X_1... ..._1+a_{12}x_2\\ X_2=a_{20}x_0+a_{21}x_1+a_{22}x_2 \end{array}$$

のように，一次式で定義される変換が， そのようなものになる．

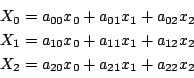
これは2直線を交点とともに2直線に移す． 2点を通る直線を2点とともに直線に移す．

逆にこのような変換はすべて上のように書ける．

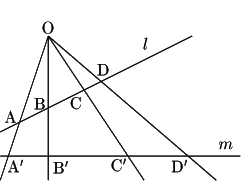射影変換を図形的に見ると， 変換ごとに図のように1点$\mathrm{O}$があって， 点$\mathrm{O}$を通る直線上の点を同じ直線上に移し， そのとき直線$l$上にある点は， 再び別の直線$m$上にあるように移る．

このような変換で 直線$l$が直線$m$に移り， $l$上の4点 $\mathrm{A},\ \mathrm{B},\ \mathrm{C},\ \mathrm{D}$が $m$上の4点 $\mathrm{A}',\ \mathrm{B}',\ \mathrm{C}',\ \mathrm{D}'$に 移ったとすると，

$$\dfrac{\mathrm{AC}}{\mathrm{CB}}：\dfrac{\mathrm{AD}}{\mathr... ...m{A'C'}}{\mathrm{C'B'}} ：\dfrac{\mathrm{A'D'}}{\mathrm{D'B'}}$$

が成り立つ．

この比のことを，4点の複比という． 射影変換で，複比は不変である．

複比の不変性を用いてパップスの定理を証明することもできる．

射影変換と複比に関するこれらのことはここでは示さない． いくつかの参考書を見てほしい．