モンジュ点

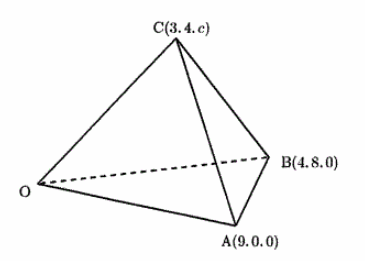
耕一　 2020年信州大学教育学部で次の問題が出ました．

$ c $ を正の実数とする．空間において，原点 $ \mathrm{O} $ および3点 $ \mathrm{A}(9,0,0) $ ， $ \mathrm{B}(4,8,0) $ ， $ \mathrm{C}(3,4,c) $ を頂点とする四面体 $ \mathrm{OABC} $ がある。 辺 $ \mathrm{OA} $ の中点 $ \mathrm{L} $ を通り直線 $ \mathrm{BC} $ に直交する平面を $ \alpha $ ， 辺 $ \mathrm{OC} $ の中点 $ \mathrm{M} $ を通り直線 $ \mathrm{AB} $ に直交する平面を $ \beta $ ， 辺 $ \mathrm{AB} $ の中点 $ \mathrm{N} $ を通り直線 $ \mathrm{OC} $ に直交する平面を $ \gamma $ とする。 次の問いに答えなさい。

(1)　平面 $ \alpha $ ， $ \beta $ ， $ \gamma $ の交点を $ \mathrm{X} $ とする。点 $ \mathrm{X} $ の座標を求めなさい。
(2)　辺 $ \mathrm{OB} $ の中点を通り，直線 $ \mathrm{AC} $ に直交する平面上に点 $ \mathrm{X} $ はあるか。 理由を述べて答えなさい。
(3)　点 $ \mathrm{X} $ が四面体 $ \mathrm{OABC} $ の表面および内部にあるような $ c $ の値の範囲を求めなさい。

(1)　 辺 $ \mathrm{OA} $ の中点 $ \mathrm{L} $ を通り直線 $ \mathrm{BC} $ に直交する平面とは， 辺 $ \mathrm{OA} $ の中点 $ \mathrm{L} $ を通り $ \overrightarrow{\mathrm{BC}} $ を法線方向とする平面である． よって $ \overrightarrow{\mathrm{BC}}=(-1,\ -4,\ c) $ より，その方程式は， \[ -\left(x-\dfrac{9}{2} \right)-4y+cz=0 \] 同様に， $ \beta $ ， $ \gamma $ の方程式は \[ \begin{array}{l} -5\left(x-\dfrac{3}{2} \right)+8(y-2)=0\\ 3\left(x-\dfrac{13}{2} \right)+4(y-4)+cz=0 \end{array} \] である．つまり， \[ \left\{ \begin{array}{l} x+4y-cz=\dfrac{9}{2}\\ 5x-8y=\dfrac{17}{2}\\ 3x+4y+cz=\dfrac{71}{2} \end{array} \right. \] これを解いて，点 $ \mathrm{X} $ の座標は \[ (x,\ y,\ z)=\left(\dfrac{7}{2},\ \dfrac{13}{4},\ \dfrac{12}{c} \right) \] である．

(2)　 同様に，辺 $ \mathrm{OB} $ の中点を通り，直線 $ \mathrm{AC} $ に直交する平面の方程式は， $ \overrightarrow{\mathrm{AC}}=(-6,\ 4,\ c) $ より， \[ -6(x-2)+4(y-4)+cz=0 \] ここに点 $ \mathrm{X} $ の座標を代入すると， \[ -6\left(\dfrac{7}{2}-2 \right)+4\left(\dfrac{13}{4}-4\right)+c\cdot\dfrac{12}{c} =-9-3+12=0 \] より，この平面上に点 $ \mathrm{X} $ はある．

(3)　 \[ \overrightarrow{\mathrm{OP}}= \alpha\overrightarrow{\mathrm{OA}}+ \beta\overrightarrow{\mathrm{OB}}+ \gamma\overrightarrow{\mathrm{OC}} \] で点 $ \mathrm{P} $ を定めるとき，点 $ \mathrm{P} $ が四面体 $ \mathrm{OABC} $ の表面および内部にある条件は， \[ \alpha,\ \beta,\ \gamma\geqq 0,\ \alpha+\beta+\gamma\leqq 1 \] である． \[ \overrightarrow{\mathrm{OX}}=\left(\dfrac{7}{2},\ \dfrac{13}{4},\ \dfrac{12}{c} \right) =\left(\dfrac{5}{24} -\dfrac{4}{3c^2}\right)(9,0,0) +\left(\dfrac{13}{32}-\dfrac{6}{c^2}\right)(4,8,0) +\dfrac{12}{c^2}(3,4,c) \] なので， \[ \dfrac{13}{32}-\dfrac{6}{c^2}\geqq 0,\ \quad \dfrac{5}{24} -\dfrac{4}{3c^2}+\dfrac{13}{32}-\dfrac{6}{c^2}+\dfrac{12}{c^2}\leqq 1 \] $ c>0 $ なので，これより $ \dfrac{8\sqrt{39}}{13}\leqq c $ を得る．

南海　一般に，次のことが成り立つ． \[ 四面体の各辺の中点を通り，対辺と垂直な6平面は，1点を共有する． \] この点をモンジュ点という．
証明1　1頂点を原点にとり，他の3頂点を \[ \mathrm{A}(a_1,\ a_2,\ a_3),\quad \mathrm{B}(b_1,\ b_2,\ b_3),\quad \mathrm{C}(c_1,\ c_2,\ c_3) \] とする．各辺の中点を通り，対辺の方向ベクトルを法線方向とする6平面の方程式は次のようになる． \[ \begin{array}{ll} (c_1-b_1)\left(x-\dfrac{a_1}{2} \right)+(c_2-b_2)\left(y-\dfrac{a_2}{2} \right) +(c_3-b_3)\left(z-\dfrac{a_3}{2} \right)=0&\cdots�@\\ (a_1-c_1)\left(x-\dfrac{b_1}{2} \right)+(a_2-c_2)\left(y-\dfrac{b_2}{2} \right) +(a_3-c_3)\left(z-\dfrac{b_3}{2} \right)=0&\cdots�A\\ (b_1-a_1)\left(x-\dfrac{c_1}{2} \right)+(b_2-a_2)\left(y-\dfrac{c_2}{2} \right) +(b_3-a_3)\left(z-\dfrac{c_3}{2} \right)=0&\cdots�B\\ c_1\left(x-\dfrac{a_1+b_1}{2} \right)+c_2\left(y-\dfrac{a_2+b_2}{2} \right) +c_3\left(z-\dfrac{a_3+b_3}{2} \right)=0&\cdots�C\\ b_1\left(x-\dfrac{c_1+a_1}{2} \right)+b_2\left(y-\dfrac{c_2+a_2}{2} \right) +b_3\left(z-\dfrac{c_3+a_3}{2} \right)=0&\cdots�D\\ a_1\left(x-\dfrac{b_1+c_1}{2} \right)+a_2\left(y-\dfrac{b_2+c_2}{2} \right) +a_3\left(z-\dfrac{b_3+c_3}{2} \right)=0&\cdots�E \end{array} \] これより， \[ \begin{array}{ll} (c_1-b_1)x+(c_2-b_2)y+(c_3-b_3)z =\dfrac{a_1(c_1-b_1)}{2}+\dfrac{a_2(c_2-b_2)}{2}+\dfrac{a_3(c_3-b_3)}{2} &\cdots�@\\ (a_1-c_1)x+(a_2-c_2)y+(a_3-c_3)z =\dfrac{b_1(a_1-c_1)}{2}+\dfrac{b_2(a_2-c_2)}{2}+\dfrac{b_3(a_3-c_3)}{2} &\cdots�A\\ (b_1-a_1)x+(b_2-a_2)y+(b_3-a_3)z =\dfrac{c_1(b_1-a_1)}{2}+\dfrac{c_2(b_2-a_2)}{2}+\dfrac{c_3(b_3-a_3)}{2} &\cdots�B\\ c_1x+c_2y+c_3z =\dfrac{c_1(a_1+b_1)}{2}+\dfrac{c_2(a_2+b_2)}{2}+\dfrac{c_3(a_3+b_3)}{2} &\cdots�C\\ b_1x+b_2y+c_3z =\dfrac{b_1(c_1+a_1)}{2}+\dfrac{b_2(c_2+a_2)}{2}+\dfrac{b_3(c_3+a_3)}{2} &\cdots�D\\ a_1x+a_2y+a_3z =\dfrac{a_1(b_1+c_1)}{2}+\dfrac{a_2(b_2+c_2)}{2}+\dfrac{a_3(b_3+c_3)}{2} &\cdots�E \end{array} \] となる．
$ �C式-�D式=�@式 $ ， $ �E式-�C式=�A式 $ ， $ �D式-�E式=�B式 $ なので， $ �C $ ， $ �D $ ， $ �E $ を満たす $ x,\ y,\ z $ は $ �@ $ ， $ �A $ ， $ �B $ も満たす．
$ \overrightarrow{\mathrm{OA}} $ ， $ \overrightarrow{\mathrm{OB}} $ ， $ \overrightarrow{\mathrm{OC}} $ は1次独立なので， \[ \left| \begin{array}{ccc} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{array} \right| \ne 0 \] である．よって，連立方程式 $ �C $ ， $ �D $ ， $ �E $ は1つの解をもつ． この点が6平面で共有される点である．

証明2　 四面体 $ \mathrm{ABCD} $ の外心を $ \mathrm{O} $ とし， $ \overrightarrow{\mathrm{OA}}=\overrightarrow{a} $ ， $ \overrightarrow{\mathrm{OB}}=\overrightarrow{b} $ ， $ \overrightarrow{\mathrm{OC}}=\overrightarrow{c} $ $ \overrightarrow{\mathrm{OD}}=\overrightarrow{d} $ とする． $ \overrightarrow{x}=(x,\ y,\ z) $ とする．
各辺の中点を通り，対辺の方向ベクトルを法線方向とする6平面のベクトル方程式は次のようになる． \[ \begin{array}{lll} \left(\overrightarrow{a}-\overrightarrow{b} \right) \cdot\left(\overrightarrow{x}-\dfrac{\overrightarrow{c}+\overrightarrow{d}}{2} \right)=0,\ & \left(\overrightarrow{a}-\overrightarrow{c} \right) \cdot\left(\overrightarrow{x}-\dfrac{\overrightarrow{b}+\overrightarrow{d}}{2} \right)=0,\ & \left(\overrightarrow{a}-\overrightarrow{d} \right) \cdot\left(\overrightarrow{x}-\dfrac{\overrightarrow{b}+\overrightarrow{c}}{2} \right)=0,\ &\\ \left(\overrightarrow{b}-\overrightarrow{c} \right) \cdot\left(\overrightarrow{x}-\dfrac{\overrightarrow{a}+\overrightarrow{d}}{2} \right)=0,\ & \left(\overrightarrow{b}-\overrightarrow{d} \right) \cdot\left(\overrightarrow{x}-\dfrac{\overrightarrow{a}+\overrightarrow{c}}{2} \right)=0,\ & \left(\overrightarrow{c}-\overrightarrow{d} \right) \cdot\left(\overrightarrow{x}-\dfrac{\overrightarrow{a}+\overrightarrow{b}}{2} \right)=0 \end{array} \] \[ |\overrightarrow{a}|= |\overrightarrow{b}|= |\overrightarrow{c}|= |\overrightarrow{d}| \] なので， \[ \overrightarrow{x}=\dfrac{1}{2}\left(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d} \right) \] は，この6式を満たす．つまり6平面は1点を共有する．

※　 垂心が存在する四面体，これを直辺四面体という．
直辺四面体については『数学対話』「特別な四面体」「直辺四面体」を参照のこと．
その定理2にあるように，直辺四面体の垂心 $ \mathrm{H} $ は， \[ \overrightarrow{\mathrm{OH}}=\dfrac{1}{2}\left(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d} \right) \] となる．これから直辺四面体では，モンジュ点は垂心に一致する．
上記定理2によらず，直接示すこともできる．
ここで改めて四面体を $ \mathrm{OABC} $ とし， $ \overrightarrow{\mathrm{OA}}=\overrightarrow{a} $ ， $ \overrightarrow{\mathrm{OB}}=\overrightarrow{b} $ ， $ \overrightarrow{\mathrm{OC}}=\overrightarrow{c} $ とする．
直辺四面体では，3組の対辺がそれぞれ直交する．すなわち \[ \overrightarrow{a}\cdot\left(\overrightarrow{b}-\overrightarrow{c} \right)=0,\ \quad \overrightarrow{b}\cdot\left(\overrightarrow{c}-\overrightarrow{a} \right)=0,\ \quad \overrightarrow{c}\cdot\left(\overrightarrow{a}-\overrightarrow{b} \right)=0 \] すなわち， \[ \overrightarrow{a}\cdot\overrightarrow{b}= \overrightarrow{b}\cdot\overrightarrow{c}= \overrightarrow{c}\cdot\overrightarrow{a} \] である．この値を$A$とおくと，6平面の方程式は \[ \begin{array}{lll} \left(\overrightarrow{c}-\overrightarrow{b} \right) \cdot\overrightarrow{x}=0 \cdots�@& \left(\overrightarrow{a}-\overrightarrow{c} \right) \cdot\overrightarrow{x}=0 \cdots�A& \left(\overrightarrow{b}-\overrightarrow{a} \right) \cdot\overrightarrow{x}=0 \cdots�B\\ \overrightarrow{c}\cdot\overrightarrow{x}=A \cdots�C& \overrightarrow{b}\cdot\overrightarrow{x}=A \cdots�D& \overrightarrow{a}\cdot\overrightarrow{x}=A \cdots�E \end{array} \] で，第 $ �C $ 式は \[ \overrightarrow{c}\cdot(\overrightarrow{x}-\overrightarrow{a})=0,\ \quad \overrightarrow{c}\cdot(\overrightarrow{x}-\overrightarrow{b})=0 \] を意味し，他の式も合わせると，各頂点と $ \overrightarrow{x} $ で定まる点を結ぶ直線が対面と直交すること示している．
よって，モンジュ点は垂心である．