四面体
拓生 外接球は,四面体を包む大きい球の半径をだんだんと小さくしていき, 頂点にぶつかるたびに少し動かしていけば,最後に4頂点が乗った球が出来そうです. 内接球も,四面体の中に含まれる小さい球の半径を大きくしていき, 面に接するたびに少し動かしていけば,最後に4面に接する球が出来そうです. 両方とも存在するようですが.
南海 重心のように明示的に書くのは簡単ではないが,存在そのものを図形的に示すことはできる. 考えてみよう.
南海 外心とは,どんなものか.
拓生 各頂点への距離が等しい点です. 空間にある2点から距離の等しい点は,2点を結ぶ線分の 垂直二等分平面です.これをもとにすればできそうですか.
証明
2頂点
![]() の中点を
の中点を![]() とし,
とし,
![]() を通り直線
を通り直線![]() に垂直な平面
に垂直な平面![]() を考える.
を考える.
![]() は2点
は2点
![]() からの距離が等しい点の集合である.
からの距離が等しい点の集合である.
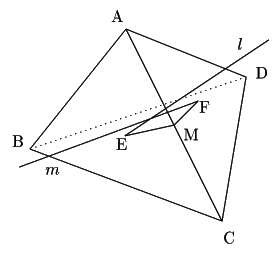
![]() の外心を
の外心を![]() とし,
とし,
![]() をとおり
をとおり
![]() に垂直な直線を
に垂直な直線を![]() とする.
とする.
![]() の外心を
の外心を![]() とし,
とし,
![]() をとおり
をとおり
![]() に垂直な直線を
に垂直な直線を![]() とする.
とする.
![]() 上の点は3点
上の点は3点
![]() から等距離にあるので,
から等距離にあるので,![]() は平面
は平面![]() 上にある.
上にある.
![]() 上の点は3点
上の点は3点
![]() から等距離にあるので,
から等距離にあるので,![]() は平面
は平面![]() 上にある.
上にある.
![]() と
と
![]() 平行でないので
平行でないので![]() と
と![]() も平行でない.
も平行でない.
ゆえに![]() と
と![]() は平面
は平面![]() 上で交わる.交点を
上で交わる.交点を![]() とすれば,
とすれば,![]() は4頂点から
等距離にあり,四面体の外心である.
は4頂点から
等距離にあり,四面体の外心である.
内心も同様に考えます.一般に平行でない2つの平面に対して,
2平面への距離が等しい点の集合は2つの平面になります.
これは図形的にも明らかですが,座標でも示せます.つまり2つの平面を