四面体![]() で,各頂点から対面への4本の垂線が1点で交わるとき,
その交点を四面体
で,各頂点から対面への4本の垂線が1点で交わるとき,
その交点を四面体![]() の垂心という.すぐにわかるが,4本の垂線のうち3本が1点で交われば
他の1垂線も同じ点で交わる.これも含めて,次の問題を考えてほしい.
の垂心という.すぐにわかるが,4本の垂線のうち3本が1点で交われば
他の1垂線も同じ点で交わる.これも含めて,次の問題を考えてほしい.
次の各命題
証明
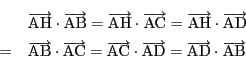
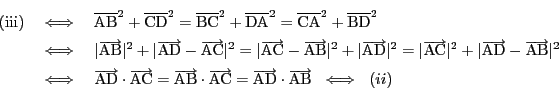
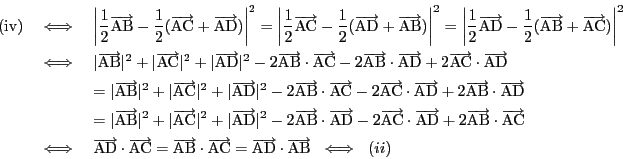
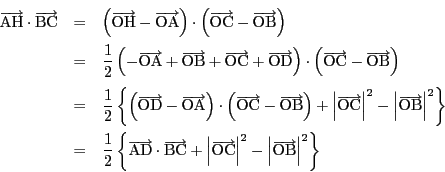
南海
この証明の最後の部分から,直辺四面体においては
その外心をO,重心をG,垂心をHとすれば
さて(i)と(ii)の同値性は次のように,図形の論証としても出来る. これは大切であるからここで紹介しよう.
(i)と(ii)の同値性の図形的証明
記号は上の証明で定めたものを使う.
四面体![]() に垂心が存在するので
頂点
に垂心が存在するので
頂点![]() から対面への垂線と
頂点
から対面への垂線と
頂点![]() から対面への垂線は交わる.
その結果,辺
から対面への垂線は交わる.
その結果,辺![]() と頂点
と頂点![]() から対面への垂線および
頂点
から対面への垂線および
頂点![]() から対面への垂線は同一平面
から対面への垂線は同一平面![]() 上にある.
上にある.
頂点![]() から対面への垂線は,
から対面への垂線は,
![]() に垂直なので
特に
に垂直なので
特に![]() と直交する.
頂点
と直交する.
頂点![]() から対面への垂線は,
から対面への垂線は,
![]() に垂直なので
特に
に垂直なので
特に![]() と直交する.
ゆえに
と直交する.
ゆえに![]() と
と![]() は直交する.辺
は直交する.辺![]() は平面
は平面![]() 上にある.
上にある.
![]() と
と
![]() は直線ABを含み,
かつCDと直交するので一致する.
よって
は直線ABを含み,
かつCDと直交するので一致する.
よって![]() と
と![]() は交わる.
同様に
C,Dから対辺への垂線の足を
は交わる.
同様に
C,Dから対辺への垂線の足を
![]() とすると,
とすると,
![]() と
と![]() ,
,![]() も交わり,
交点はすべて
も交わり,
交点はすべて![]() 上にある.
上にある.
AをBに代えることで![]() と
と
![]() ,
,![]() ,
,![]() も交わり,
交点はすべて
も交わり,
交点はすべて![]() 上にある.
上にある.
よって![]() ,
,![]() は
は![]() と
と![]() の交点を通り4垂線は1点で交わる.
の交点を通り4垂線は1点で交わる.
拓生
AHは
![]() と直交するので特にCDと直交する.
ABもCDと直交するので,AHはABをとおりCDに直交する平面上にある.
と直交するので特にCDと直交する.
ABもCDと直交するので,AHはABをとおりCDに直交する平面上にある.
![]() もこの平面上にあるので,
その結果
もこの平面上にあるので,
その結果
![]() となり,同様に
となり,同様に
![]() も示され,
も示され,![]() は
は
![]() の垂心である.
の垂心である.
![]() の頂点Aから対辺CDに降ろした垂線も,
の頂点Aから対辺CDに降ろした垂線も,
![]() の頂点Bから対辺CDに降ろした垂線も,
ABをとおりCDに直交する平面上にある.
よってその足はこの平面とCDの交点であり,同一の点である.
の頂点Bから対辺CDに降ろした垂線も,
ABをとおりCDに直交する平面上にある.
よってその足はこの平面とCDの交点であり,同一の点である.
拓生 対辺直交なので
 南海
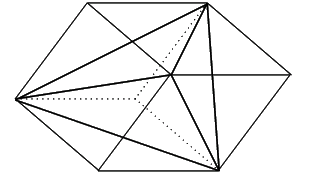
直辺四面体を埋め込む平行六面体はどのようなものか.
南海
直辺四面体を埋め込む平行六面体はどのようなものか.
拓生 平行六面体の対面の対角線が,四面体の対辺となりそれが直交するのだから, 平行六面体の隣り合う辺の長さが等しい. これがいずれについても言えるので, その平行六面体はすべての辺の長さが等しい平行六面体(等辺長六面体)です.
6面が辺長の等しいひし形から出来ています.
南海 逆に,辺長の等しいひし形を,同じ形のもの2枚ずつ用意し, それで平行六面体を作ると, そこから直辺四面体が得られる.