三角形ABCにおいて,各辺の中点の3点, 各頂点から対辺への垂線の足3点, 各頂点と垂心の中点3点のあわせて9点を通る円が存在する. これを九点円という. 外接円の半径をこれは入試問題にもあります. それは『九点円の不思議』にあります.とすると, 九点円の半径は
であり,中心は外心と垂心の中点である.
この『九点円の不思議』に書かれていることは, 垂心のある四面体,直辺四面体に拡張されるのでしょうか.
南海 フォイエルバッハの定理に相等するものについては知らない.今後の課題としておこう. その前にそもそも九点円に対応するものがあるのか,が問題だ. これについては次のことが知られている. 『幾何学大辞典』第二巻(岩田至康編,182ページ)に載っている.
南海 第1種の十二点球を各面で切ったものは,その面の九点円そのものであるから, それぞれの面の垂心と頂点の中点3点,合計12点も通り,24点球ともいわれることもある. 『幾何学大辞典』には図形の論証とベクトルを用いた証明の概略が載っている.
拓生 直辺四面体の定理ですね.
南海
そうだ.
その証明で論証上必要なところだけを取り出せば,
一般の四面体の定理にすることが出来る.
滋賀県彦根東高校の高校生四人がそれを考えた.
それが雑誌『初等数学』2012年1月号に載っている.
『幾何学大辞典』にも,「(ii)はそのまま![]() 次元の場合に拡張される」と書いてある.
次元の場合に拡張される」と書いてある.
『九点円の不思議』の最初の部分,九点円の存在証明を踏まえ,
(i),(ii)を証明しよう.
その上で,![]() 次元の一般の四面体の場合で定理を記述し,
証明しよう.
次元の一般の四面体の場合で定理を記述し,
証明しよう.
拓生
まず(i)をやってみます.
この場合,12点を通る球があるとし,
四面体の外心,その球の中心,垂心の3点を
![]() に
正射影すれば,その球の中心の射影が
に
正射影すれば,その球の中心の射影が
![]() の
九点円の中心であるはずで,それは三角形の外心と垂心の中点です.
の
九点円の中心であるはずで,それは三角形の外心と垂心の中点です.
ですから12点球の中心も四面体の外心と垂心の中点, つまり四面体の重心であろうと推測されます. そこで,重心と辺の中点との距離を調べました.
定理3(i)証明
外接球の半径を![]() ,外心をOとし,垂心をHとする.
,外心をOとし,垂心をHとする.
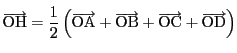 であった.さらにOとHの中点は四面体ABCDの重心Gである.
辺ABの中点とGの距離は
であった.さらにOとHの中点は四面体ABCDの重心Gである.
辺ABの中点とGの距離は
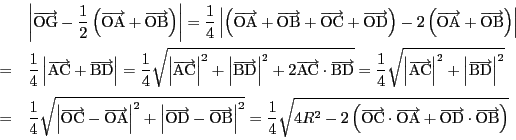
よってこの6点はGを中心とする球面上にある.
この球面と
![]() で定まる平面との共通部分は
で定まる平面との共通部分は
![]() の各辺の中点を通る円である.
つまり
の各辺の中点を通る円である.
つまり
![]() の九点円である.
九点円はその三角形の各頂点から対辺への垂線の足を通る.
系1によって共通垂線の足は三角形の各頂点から対辺への垂線の足
であるから,この球はこれら6個の共通垂線の足も通る.
□
の九点円である.
九点円はその三角形の各頂点から対辺への垂線の足を通る.
系1によって共通垂線の足は三角形の各頂点から対辺への垂線の足
であるから,この球はこれら6個の共通垂線の足も通る.
□
南海
この球の半径が
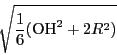
拓生
次に(ii)に進みます.
九点円の場合からの推測で,
頂点Aと垂心Hを![]() に内分する点と
に内分する点と
![]() の重心との中点が球の中心ではないかと考えました.
つまり次のように九点円の証明を真似ました.
の重心との中点が球の中心ではないかと考えました.
つまり次のように九点円の証明を真似ました.
定理3(ii)証明
頂点Aと垂心Hを![]() に内分する点
に内分する点![]() と
と
![]() の重心
の重心![]() との中点をEとする.
との中点をEとする.
Aから
![]() への垂線の足を
への垂線の足を![]() とすると,球の直径が
とすると,球の直径が
![]() であり,
垂心の定義から
であり,
垂心の定義から
![]() なので,
なので,![]() もこの球面上にある.
以上から,各4点ずつ12個の点はEを中心とする半径
もこの球面上にある.
以上から,各4点ずつ12個の点はEを中心とする半径![]() の球面上にある.
□
の球面上にある.
□
南海 平面三角形の場合の九点円からの自然な拡張になっているのは どちらか.
拓生 証明の方法からも(ii)の方です.