![]() 次元のユークリッド空間で考えよう.
実数
次元のユークリッド空間で考えよう.
実数![]() の
の![]() 個の組
個の組
![]() で点が定まると考えるのだ.
ここに
で点が定まると考えるのだ.
ここに![]() 個の点
個の点
![]() があるとする.
この
があるとする.
この![]() 個の識別と座標成分の識別を明確にするときは,次のように書く.
個の識別と座標成分の識別を明確にするときは,次のように書く.
拓生
上につけるのですね.
これら![]() 個の点は,同じ平面上にあったりしてはいけないですね.
個の点は,同じ平面上にあったりしてはいけないですね.
南海
これら![]() 個の点のどの3点も同一直線上にはないとする.
これを一般の位置にあるという.
個の点のどの3点も同一直線上にはないとする.
これを一般の位置にあるという.
拓生
![]() 面体でも重心Gは,
面体でも重心Gは,
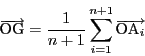
しかし外心の存在は明らかではないです. 2011年の京都大学で外心の存在を示せという問題が出ました. 4通りの解答を学びました.
南海 解の3を使うと数学的帰納法で出来ないか.
拓生 確かに.
![]() のときは三角形の外心である.
のときは三角形の外心である.
![]() のとき成立とする.
のとき成立とする.![]() のときの成立を示す.
のときの成立を示す.![]() 次元空間で考える.
座標は先と同様とする.
次元空間で考える.
座標は先と同様とする.
数学的帰納法の仮定から,
![]() 個の点
個の点
![]() のうち,
のうち,
![]() 個の点
個の点
![]() から等距離
から等距離![]() にある点は存在する.その点を
にある点は存在する.その点を
![]() とする.
任意の実数
とする.
任意の実数![]() に対して,点
に対して,点
![]() は方程式
は方程式
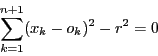
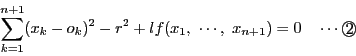
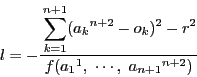
垂心が存在すれば![]() のときと同様に,すべて異なる任意の
のときと同様に,すべて異なる任意の
![]() に対して
に対して
拓生
逆にこのとき,点Hを
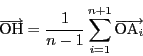

南海 その前に(ii)を一般化して定式化してほしい.
拓生 はい.
![]() 次元空間に
次元空間に![]() 面体
面体
![]() がある.
その外心をO,外接球の半径を
がある.
その外心をO,外接球の半径を![]() とする.その垂心が存在するとし,それをHとする.
とする.その垂心が存在するとし,それをHとする.
![]() 個の頂点から一つを除いた他の点で定まる
個の頂点から一つを除いた他の点で定まる![]() 次空間を,
この
次空間を,
この![]() 面体の面という.
面体の面という.
各面の重心![]() 点,各頂点から対面への垂線の足
点,各頂点から対面への垂線の足![]() 点,
頂点と垂心を
点,
頂点と垂心を![]() に内分する点
に内分する点![]() 点の
点の![]() 点は同一球面上にある.
■
点は同一球面上にある.
■
証明
頂点![]() と垂心Hを
と垂心Hを![]() に内分する点
に内分する点![]() と
面
と
面
![]() の重心
の重心![]() との中点をEとする.
との中点をEとする.
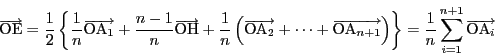
![]() から面
から面
![]() への垂線の足を
への垂線の足を![]() とすると,球の直径が
とすると,球の直径が
![]() であり,
垂心の定義から
であり,
垂心の定義から
![]() なので,
なので,![]() もこの球面上にある.
以上から,各
もこの球面上にある.
以上から,各![]() 点ずつ
点ずつ![]() 個の点はEを中心とする半径
個の点はEを中心とする半径![]() の球面上にある.
□
の球面上にある.
□
拓生 垂心が存在しなくても,一定の定理にすることが出来るのですか.
南海 そこが彦根東高校の高校生が考えたところで, この証明で使ったところだけを引き出すと,次のようにまとめることが出来る.
![]() 次元空間に
次元空間に![]() 面体
面体
![]() がある.
その外心をO,外接球の半径を
がある.
その外心をO,外接球の半径を![]() とする.
点Hを
とする.
点Hを
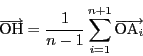
拓生 そうか.これで証明に使ったことは全てはいっていますね.
南海 こういうことを考えている 高校生がいるということは,たいへん嬉しいことだ.