四面体
- 4つの面の面積がすべて等しい.
- 4つの面はすべて合同である.
拓生 4面合同な四面体はこれまでにも見たことがあります.(ii)から(i)は明らかだから, (i)から(ii)を示すのですね.
南海 4つの面が合同な四面体を等面四面体という. 等積四面体は等面四面体である,これが定理の核心だ.証明はいろいろな方法がある.2通りの方法で示そう.
証明
方針は次の通り.
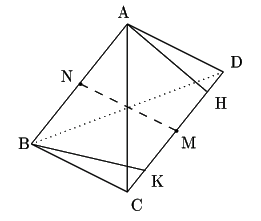 点
点![]() から辺
から辺![]() におろした垂線の足を
におろした垂線の足を![]() ,
点
,
点![]() から辺
から辺![]() におろした垂線の足を
におろした垂線の足を![]() とする.
とする.
![]() と
と
![]() の面積が等しいので,
の面積が等しいので,
![]() である.
である.
このとき
![]() を示す.これが示せれば三平方の定理から
を示す.これが示せれば三平方の定理から
![]() となる.
となる.
![]() ,
,
![]() も同様に示される.よって対辺の長さがそれぞれ等しく,4面の三角形は対応する3辺の長さが
それぞれ等しくなり,合同である.
も同様に示される.よって対辺の長さがそれぞれ等しく,4面の三角形は対応する3辺の長さが
それぞれ等しくなり,合同である.
そのために線分![]() の中点
の中点![]() をとる.
をとる.![]() をとおり直線
をとおり直線![]() に
垂直な平面を
に
垂直な平面を![]() とする.
とする.![]() と直線
と直線![]() の交点を
の交点を![]() とする.
直線
とする.
直線![]() は
は![]() をとおり
をとおり![]() と平行な平面上にあり,
直線
と平行な平面上にあり,
直線![]() は
は![]() をとおり
をとおり![]() と平行な平面上にある.
と平行な平面上にある.![]() が
線分
が
線分![]() の中点なので,これら2つの平面は
の中点なので,これら2つの平面は![]() から等距離にある.
から等距離にある.
したがって点![]() から
から![]() への距離と,点
への距離と,点![]() から
から![]() への距離は等しい.
ゆえに,点
への距離は等しい.
ゆえに,点![]() は線分
は線分![]() の中点である.
の中点である.![]() は
は![]() 上の直線なので
上の直線なので
ねじれの位置にある2直線の両方に直交する直線はただ一つしかない.したがって
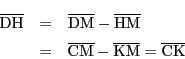
拓生 よくわかりました.しかし巧みな証明です. ただ,「ねじれの位置にある2直線の両方に直交する直線はただ一つしかない」 ことが,直感的には明らかですが,厳密にはどのようにすればよいのでしょうか.
南海 それは『高校数学の方法』「同値変形で問題を解きほぐす」の演習問題2を見てほしい.
さて考え方は同じなのだがこれを座標でやってみよう. そのために次の事実が必要だ.
空間に2つのベクトル
拓生
やってみます.
![]() とします.
とします.
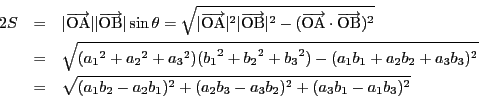
別証明
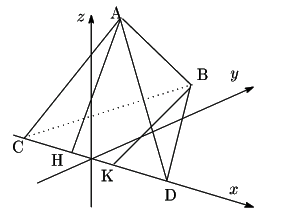 四面体
四面体![]() を,図のように辺
を,図のように辺![]() の中点を原点に,
点
の中点を原点に,
点![]() を
を![]() 平面上に置いて,
平面上に置いて,![]() 座標空間に置く.
ただし,
座標空間に置く.
ただし,
点![]() から
から![]() への垂線の足を
への垂線の足を![]() ,
点
,
点![]() から
から![]() への垂線の足を
への垂線の足を![]() とすると,その座標は
とすると,その座標は
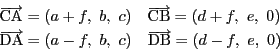
南海 じつはこのような位置に置かなくても, 3次行列やベクトルの外積といわれるものを使う証明方法がある. それは『線型幾何入門』の中にある.
等面四面体は四面体のなかで最も美しいものだ. この等面四面体を埋め込む平行六面体は何か.
拓生 六面体の各面は平行四辺形だが等面四面体では,対角線が等しい. 対角線の長さが等しい平行四辺形は長方形なので,それは直方体です.
南海 直接的な証明などは『高校数学の方法』「存在の証明」のなかにある. これも参考にしてほしい.
最後に,最初の京大の問題だが,条件(i)は埋め込み平行六面体が等辺長六面体であるということであり, 条件(ii)は埋め込み平行六面体が直方体であるということになった.したがって(i)かつ(ii)になるのは 埋め込み平行六面体が立方体ということだ.これは正四面体だ.
拓生 別解です.
南海 この問題を解くのにこの方法はまわりくどいから別解とはいえないが,しかしこの 平行六面体を考えることで問題の意義を理解することができる.