拓生 他にもあるということですか.
南海
三角形で,重心![]() ,外心
,外心![]() ,内心
,内心![]() のうち2つが一致すると?
のうち2つが一致すると?
拓生
正三角形です.
![]() で
で
重心は頂点![]() と対辺
と対辺![]() の中点を結ぶ直線上にあり,
外心は辺
の中点を結ぶ直線上にあり,
外心は辺![]() の垂直二等分線上にある.
これが一致すれば,頂点と対辺の中点を結ぶ直線とその辺が直交し,
の垂直二等分線上にある.
これが一致すれば,頂点と対辺の中点を結ぶ直線とその辺が直交し,
![]() の二等辺三角形.
これが2つの頂点についても成り立つので正三角形.
の二等辺三角形.
これが2つの頂点についても成り立つので正三角形.
3つの三角形
![]() ,
,
![]() ,
,
![]() は面積が等しい.
さらに重心と内心が一致すれば,
は面積が等しい.
さらに重心と内心が一致すれば,
![]() と
これら3つの三角形の辺
と
これら3つの三角形の辺
![]() ,
,
![]() ,
,
![]() に下ろした垂線の足までの長さが等しい.つまり3つの三角形の高さが等しい.
よって底辺が等しく
に下ろした垂線の足までの長さが等しい.つまり3つの三角形の高さが等しい.
よって底辺が等しく
![]() が示された.
が示された.
辺![]() の中点を
の中点を![]() とし,
外接円,内接円の半径をそれぞれ
とし,
外接円,内接円の半径をそれぞれ![]() とする.
とする.
このとき
![]() となる.
右辺は辺の選び方によらない定数なので,3辺が相等しい.
となる.
右辺は辺の選び方によらない定数なので,3辺が相等しい.
南海 そうだ.では,四面体で重心と外心が一致すると?
拓生 正四面体ですか.
南海 ところがそうではない.ここが三角形と四面体の違うところだ.
四面体で重心と外心が一致すると,それは等面四面体なのだ.実は次のことが成り立つ.
証明
以下の証明で,四面体![]() の
重心を
の
重心を![]() ,
外心を
,
外心を![]() ,
内心を
,
内心を![]() とおく.
とおく.
先に等面四面体は直方体に埋め込まれることを示した.
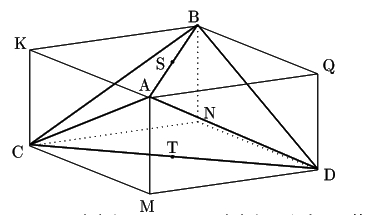 辺
辺
![]() がそれぞれ,
長方形
がそれぞれ,
長方形![]() ,
, ![]() の中心であるから,
の中心であるから,
![]() はこの直方体の中心でもある.
はこの直方体の中心でもある.
したがって![]() から4つの頂点への長さが等しく,外心でもある.
から4つの頂点への長さが等しく,外心でもある.
その結果![]() を一つの頂点とする4つの四面体
を一つの頂点とする4つの四面体
![]() は6辺が相等になりすべて合同,
よって
は6辺が相等になりすべて合同,
よって![]() から各辺への垂線の長さも等しい.
つまり
から各辺への垂線の長さも等しい.
つまり![]() は内心でもある.
は内心でもある.
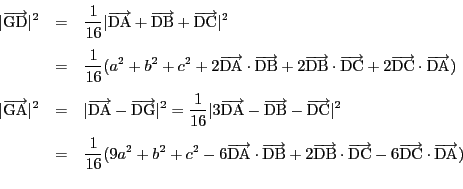
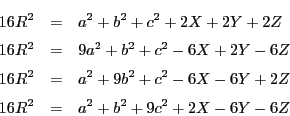
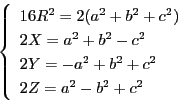
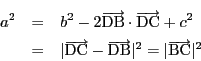
注 次の場合と同様に等積四面体であることを示すことも出来る.
![]() を他の頂点にとっても同様である.
よって
を他の頂点にとっても同様である.
よって![]() を一つの頂点とする4つの四面体
を一つの頂点とする4つの四面体
![]() ,
, ![]() ,
, ![]() ,
, ![]() の体積は,
いずれも四面体
の体積は,
いずれも四面体![]() の
の![]() であり,相等しい.
であり,相等しい.
一方重心![]() が内心
が内心![]() でもあるので,
でもあるので,
![]() から各面に下ろした垂線の長さは相等しい.
から各面に下ろした垂線の長さは相等しい.
したがって4つの四面体
![]() の,
頂点
の,
頂点![]() に対する底面の面積も相等しい.
に対する底面の面積も相等しい.
つまり四面体![]() は等積四面体である.
等積四面体は等面四面体であるので,
四面体
は等積四面体である.
等積四面体は等面四面体であるので,
四面体![]() が等面四面体であることが示された.
が等面四面体であることが示された.
 外心
外心
![]() が内心でもあるので
が内心でもあるので![]() は
内接円が四面体の面
は
内接円が四面体の面
![]() に接する点でもある.
内接円の半径を
に接する点でもある.
内接円の半径を![]() とする.
外接円の半径
とする.
外接円の半径![]() は三平方の定理から
は三平方の定理から
これは外接円と内接円で定まる定数である.ゆえに他の3つの面,
![]() ,
,
![]() ,
,
![]() の外接円の半径もすべて
の外接円の半径もすべて
![]() に等しい.
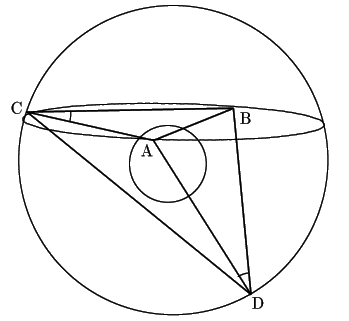
すると,弦
に等しい.
すると,弦![]() に対する同じ半径の円の円周角は等しいので
に対する同じ半径の円の円周角は等しいので
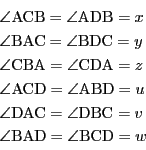
つまり四面体![]() は等面四面体である.
は等面四面体である.