力もベクトルなのでこれを
![]() と記し,
位置をベクトル
と記し,
位置をベクトル
![]() とおき,かつ
比例定数を
とおき,かつ
比例定数を![]() とすれば,
ニュートンの第2法則は,
とすれば,
ニュートンの第2法則は,
南海 今年(2006年)の入試から, 京都大学では数学III で「簡単な微分方程式及び曲線の長さ」が含まれることになった.
もともと1960年代は「微分方程式」が「積分法の応用」の中の一節としてあった. 十数年前の「微分・積分」にもあったが,それがこの十年なく,今回の改訂でも復活しなかった.
しかし,青空学園の『数学対話』−「惑星は楕円軌道を描く」を見ればわかるように,
自然界の多くの現象は,微分方程式で書かれ, それを解くことで運動の法則が分かる. というより, もともとニュートン以来, 微分法,積分法は微分方程式を解いて自然現象を解明することからはじまったのだ.
『数学対話』−「惑星は楕円軌道を描く」では
力もベクトルなのでこれを
![]() と記し,
位置をベクトル
と記し,
位置をベクトル
![]() とおき,かつ
比例定数を
とおき,かつ
比例定数を![]() とすれば,
ニュートンの第2法則は,
とすれば,
ニュートンの第2法則は,
と出てくる.これから位置をベクトル
![]() が確定し,
惑星の軌道が楕円であることが,解明されるのだった.
が確定し,
惑星の軌道が楕円であることが,解明されるのだった.
今回は,この微分方程式のごく入り口を話そう.
拓生 そもそも微分方程式とは何なのですか.
南海
原点を中心とする半径![]() の円の方程式は
の円の方程式は
拓生
南海
この関係式を未知関数![]() とその導関数
とその導関数![]() および変数
および変数![]() の定関数(この場合は
の定関数(この場合は![]() そのもの)
についての関係式と見たものが微分方程式だ.
そのもの)
についての関係式と見たものが微分方程式だ.
拓生
この関係式をみたす![]() を求めるのですね.
を求めるのですね.
南海 そうだ.
今度は逆に![]() を0でない定数として
を0でない定数として
拓生
2回微分すると
南海
このように,
未知な関数とその導関数,および定関数を含む等式を微分方程式という.
含まれる導関数の最も高い次数が![]() であるとき,これを
であるとき,これを![]() 階微分方程式という.
階微分方程式という.
関数を![]() とすると,微分方程式とは,
とすると,微分方程式とは,
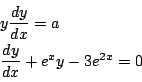
微分方程式を![]() を用いて書きあらわすことも出来る.
例えば上の等式は
を用いて書きあらわすことも出来る.
例えば上の等式は
![]() を用いて
を用いて
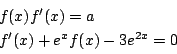
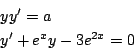
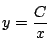
拓生 何回か微分した等式から定数を消去すればよいのですね.