


次: 微分方程式を解く
上: 微分方程式とは
前: 微分方程式
南海
与えられた微分方程式を満たす関数を微分方程式の解といい,
解を求めることを微分方程式を解くという.
微分方程式 を解いてみよう.
を解いてみよう.
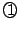 を
を
とおいて両辺を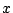 で積分するとどのようになるか.
で積分するとどのようになるか.
拓生
左辺は
と積分定数だから,まとめて
となります.つまり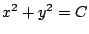 です.半径は定まりません.
です.半径は定まりません.
南海
上の計算で置換積分になっているところは
から直ちに
とし,両辺の積分をとる,として
としてよい.
このように,微分方程式を解いて表れる定数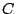 のことを任意定数という.
のことを任意定数という.
ここで,例えば
のような条件をつけると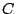 が定まる.
が定まる.
拓生
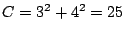 なので半径5の円になります.
なので半径5の円になります.
ところでこの微分方程式は
この方程式を満たす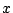 と
と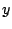 を座標にとって点
を座標にとって点
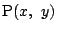 とすると,
点
とすると,
点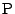 での接線の傾きが
での接線の傾きが
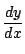 ですから,
この式は直線
ですから,
この式は直線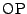 と,点
と,点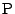 での接線が直交している,
ということを意味しています.
だから円になるのですね.
での接線が直交している,
ということを意味しています.
だから円になるのですね.
南海
微分方程式の意味はそういうことだ.
任意定数を含んだ解を一般解,
任意定数に特別の値を与えて得られる解を特殊解という.
また,任意定数を定める条件を初期条件という.
Aozora Gakuen
![]() を解いてみよう.
を解いてみよう.
![]() を
を
![]() のことを任意定数という.
のことを任意定数という.
![]() なので半径5の円になります.
なので半径5の円になります.