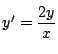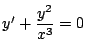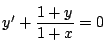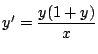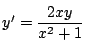高校数学で解けた方がいいのは次の場合である.
最も簡単な場合に工夫して解いてみてほしい.
例 1.2 次の微分方程式の一般解を求めよ.
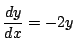
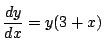
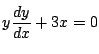
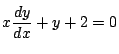
解答
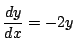 より
より
![]() のとき
のとき
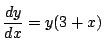 より
より
![]() のとき
のとき
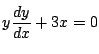 より
より
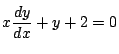 より
より
![]() のとき.
のとき.
参考までにもう少し進んだところも話しておこう.
この置換の仕方は多くの工夫がなされている. 高校数学では,それらを知る必要はないが,置換が指示されれば解けるようにしたい.
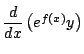 なので
なので
例えば
![]() なので両辺に
なので両辺に![]() をかける.
をかける.
南海 変数分離形を解く練習をしよう.