拓生
![]() の基本的な変数は時間
の基本的な変数は時間![]() です.
惑星の軌道は
です.
惑星の軌道は![]() と角
と角![]() の関係です.
の関係です.
時間![]() での位置を決定することはしないのですか.
での位置を決定することはしないのですか.
南海
確かにそこまでしてはじめて問題を解いたといえる.
しかし,まず
![]() から
から![]() と角
と角![]() の関係を導き,
楕円軌道であることを確定させ,観測データとあわせながら,
位置決定などの問題を解くのが現実的なのだ.
の関係を導き,
楕円軌道であることを確定させ,観測データとあわせながら,
位置決定などの問題を解くのが現実的なのだ.
そこで![]() と角
と角![]() の関係を導きたい.
の関係を導きたい.
![]() から
から
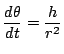 が導かれている.
これを
が導かれている.
これを![]() に代入して整理する.
に代入して整理する.
拓生
逆数の多い複雑な方程式になりました.
南海
方程式が複雑になったときは,より基本的な変数に変えてみる,ということが基本だ.
![]() は質点間の距離であるが,距離,速度,加速度,といった数学的な量に対して,
は質点間の距離であるが,距離,速度,加速度,といった数学的な量に対して,
位置エネルギー(本当は「ポテンシャル」というべき所だ),運動量,力, といった物理学的な量が,特にそれが保存量である場合に,基本的な量だ.
2つの質量![]() をもつ質点が万有引力で引き合い,距離
をもつ質点が万有引力で引き合い,距離![]() のときそれぞれ
速度が
のときそれぞれ
速度が![]() となったとする.万有引力による位置エネルギー
となったとする.万有引力による位置エネルギー![]() は
は
拓生
これはエネルギー保存則
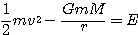
南海
この![]() は,中心力が働く場でのポテンシャルというものだ.
これはこのような場での基本量だ.
は,中心力が働く場でのポテンシャルというものだ.
これはこのような場での基本量だ.
ポテンシャルは![]() に比例している.
に比例している.
拓生
![]() と変数を変換してみる価値があるのですね.
と変数を変換してみる価値があるのですね.
南海 数学的にも, 微分方程式を変形するためのこのような置き換えは長い間にいろいろと工夫されてきたのだ. 物理的にも意義あるわけだ.
ここではそれを使わせてもらう.
![]() での微分を作ったうえで,
での微分を作ったうえで,![]() での微分に置きかえていく.
での微分に置きかえていく.
拓生
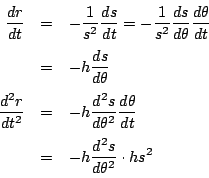
ですから![]() は
は
南海
つまり
ここで
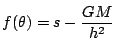 とおくと,
とおくと,
この微分方程式を解けばよい.
南海
確かに.それらは![]() をみたす.問題は
をみたす.問題は![]() を満たすものをすべて求めなければならない.
を満たすものをすべて求めなければならない.
拓生
でも
一方,
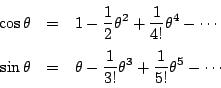
南海 よくできました.ニュートンの力学に現れる関数は何度でも微分可能で, 級数に展開できる.だからこれでよい.
ここでは, 次のようなより一般的な微分方程式の解に関する基本定理を考えておこう.
定理 2
微分方程式
![]() において
において
証明
拓生 (1)はすぐ出来ます.
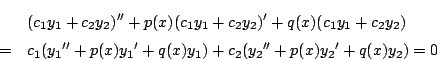
南海 (2)は少し難しい.
任意の解![]() をとる.
行列
をとる.
行列
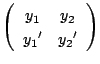 は,
は,
![]() より逆行列をもつ.
そこで
より逆行列をもつ.
そこで

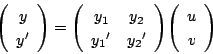
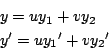
第2式を微分して
![]() となる.
ここで
となる.
ここで
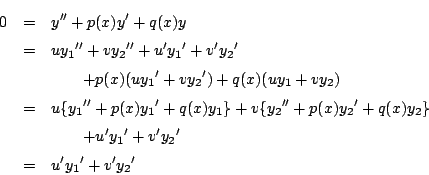
したがって
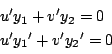
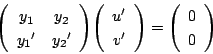
拓生
![]() とすると
とすると
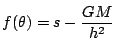 であったから
であったから
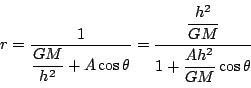
拓生
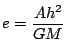 ,
,
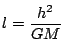 とおくと
とおくと
南海 実際に惑星の軌道は閉じているので楕円でなければならない. これがケプラーの第2法則だ.
拓生 わかりました.そうすると彗星などでは放物線になったりもするのですね.
南海 そうだ.